
 如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.分析 (1)①根据SAS即可判定.②由△OAC≌OBD,推出∠OAE=∠OBD,由△OAB是等边三角形,推出∠OAB+∠OBA=120°,推出∠OAE+∠BAE+∠OBA=120°,即∠EAB+∠EBA=120°,推出∠AEB=60°.
(2)OE平分∠AED.作OM⊥AC于M,ON⊥BD于N.由△OAC≌△OBD,推出S△OAC=S△OBD,推出$\frac{1}{2}$•AC•OM=$\frac{1}{2}$•BD•ON,推出OM=ON,再根据角平分线判定定理即可证明.
解答 (1)证明:①∵△OAB与△OCD都是等边三角形,
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
∴△OAC≌△OBD.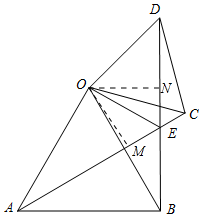
②∵△OAC≌OBD,
∴∠OAE=∠OBD,
∵△OAB是等边三角形,
∴∠OAB+∠OBA=120°,
∴∠OAE+∠BAE+∠OBA=120°,
即∠EAB+∠EBA=120°,
∴∠AEB=60°.
(2)解:OE平分∠AED.理由如下:
作OM⊥AC于M,ON⊥BD于N.
∵△OAC≌△OBD,
∴S△OAC=S△OBD,
∴$\frac{1}{2}$•AC•OM=$\frac{1}{2}$•BD•ON,
∴OM=ON,
∴OE平分∠AED.
点评 本题考查全等三角形的判定和性质、角平分线的判定等知识,解题的关键是灵活运用全等三角形的性质解决问题,学会利用面积法证明线段相等,属于中考常考题型.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:填空题
 已知正方形ABCD,M、N两动点分别从A、C两点同时出发沿正方形的边开始移动,点M按逆时针方向移动,点N按顺时针方向移动,若点M的速度是点N的4倍,则它们第2017次相遇在边AB上.
已知正方形ABCD,M、N两动点分别从A、C两点同时出发沿正方形的边开始移动,点M按逆时针方向移动,点N按顺时针方向移动,若点M的速度是点N的4倍,则它们第2017次相遇在边AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)(x+3) | B. | (x-6)(x+2) | C. | (x-4)(x-3) | D. | (x+6)(x-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com