练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    当t
     
    时，关于x的方程x2-3x+t=0可用公式法求解．
    分析：关于x的方程x2-3x+t=0可用公式法求解，则△=b2-4ac≥0，即△=32-4×1×t=9-4t≥0，解不等式即可．
    解答：解：∵关于x的方程x2-3x+t=0可用公式法求解，
    ∴△=b2-4ac≥0，即△=32-4×1×t=9-4t≥0，
    ∴t≤
    9
    4
    ．
    故答案为≤
    9
    4
    ．
    点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：单科王牌　　九年级数学(上) 题型：044

    为了预防“非典”，某学校对教室采用药薰消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例．药物燃烧后，y与x成反比例，如图所示，现测得药物8分钟燃烧完毕．此时室内空气中每立方米的含药量为6毫克，请你根据题中所提供的信息，解答下列问题：

    (1)药物燃烧时，y与x的函数关系式为________，自变量x的取值范围是________；

    (2)药物燃烧后，y关于x的函数关系式为________；

    (3)研究表明，当空气中的含药量低于1.6毫克时，学生方可进教室．那么从消毒开始，至少经过多少分钟，学生方可回到教室？

    (4)研究表明，当空气中每立方米的含药量不低于1.6毫克且持续时间不低于10分钟时，方能有效杀死空气中的病菌，那么此次消毒是否有效？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．

    1.发现C船时，A、B、C三船所在位置的坐标分别为A(_______，_______)、B(_______，_______)和C(_______，_______)；

    2.发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题8分）如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．

       (1)发现C船时，A、B、C三船所在位置的坐标分别为A(_______，_______)、B(_______，_______)和C(_______，_______)；

    (2)发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题8分）如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．

    (1)发现C船时，A、B、C三船所在位置的坐标分别为A(_______，_______)、B(_______，_______)和C(_______，_______)；
    (2)发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011年江苏省苏州市中考模拟数学卷 题型：解答题

    （本题8分）如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．

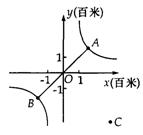
        (1)发现C船时，A、B、C三船所在位置的坐标分别为A(_______，_______)、B(_______，_______)和C(_______，_______)；

    (2)发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．

     

    查看答案和解析>>

    同步练习册答案