
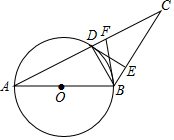
 如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.
如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.分析 (1)根据圆周角定理得到∠ADB=90°,解直角三角形得到BD=4,AD=4$\sqrt{3}$,于是得到AD=$\frac{1}{2}$AC,即可得到结论;
(2)连接OD,根据三角形中位线的性质得到OD∥BC,OD=$\frac{1}{2}$BC,推出OD⊥DE,于是得到DE是⊙O的切线;
(3)根据已知条件得到AF=$\frac{16}{3}$$\sqrt{3}$,求得DF=$\frac{4}{3}$$\sqrt{3}$,根据勾股定理即可得到结论.
解答 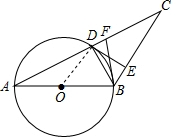 解:∵(1)∵AB是⊙O的直径,
解:∵(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵直径AB=8,∠A=30°,
∴BD=4,AD=4$\sqrt{3}$,
∵AC=8$\sqrt{3}$,
∴AD=$\frac{1}{2}$AC,
∴直线BD是线段AC的垂直平分线;
(2)连接OD,
∵D,O分别是线段AC,AB的中点,
∴OD∥BC,OD=$\frac{1}{2}$BC,
∵DE⊥BC,
∴∠DEC=∠EDO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵点F是AC的三等分点,
∴AF=$\frac{16}{3}$$\sqrt{3}$,
∵AD=4$\sqrt{3}$,
∴DF=$\frac{4}{3}$$\sqrt{3}$,
∵BD⊥AC,BD=4,
∴BF=$\sqrt{D{F}^{2}+B{D}^{2}}$=$\frac{8}{3}$$\sqrt{3}$.
点评 本题考查了切线的性质和判定,圆周角定理,勾股定理,线段垂直平分线的判定,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
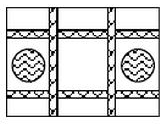 “G20峰会“将于2016年9月在抗州举行,杭州迸进行全面撤城市美化工程.小丽爸爸是一个园林设计师.将对一块长80m,宽60m的空地进行园艺设计(如图),在空地设计两纵两横相同宽度的小路,再设计两个半径为路宽2倍的圆形喷水池,喷水池和小路的面积之和占整个空地面积的$\frac{2}{15}$.
“G20峰会“将于2016年9月在抗州举行,杭州迸进行全面撤城市美化工程.小丽爸爸是一个园林设计师.将对一块长80m,宽60m的空地进行园艺设计(如图),在空地设计两纵两横相同宽度的小路,再设计两个半径为路宽2倍的圆形喷水池,喷水池和小路的面积之和占整个空地面积的$\frac{2}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
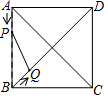 如图,正方形ABCD中,动点P的运动路线为AB→BC,动点Q的运动路线为对角线BD,点P,Q以同样的速度分别从A,B两点同时出发匀速前进,当一个点到达终点停止运动时,另一个点也随之停止.设点P的运动路程为x,PQ的长为y,则下列能大致表示y与x的函数关系的图象为( )
如图,正方形ABCD中,动点P的运动路线为AB→BC,动点Q的运动路线为对角线BD,点P,Q以同样的速度分别从A,B两点同时出发匀速前进,当一个点到达终点停止运动时,另一个点也随之停止.设点P的运动路程为x,PQ的长为y,则下列能大致表示y与x的函数关系的图象为( )| A. | 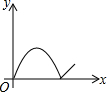 | B. | 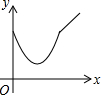 | C. |  | D. | 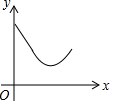 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
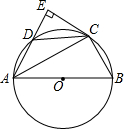 已知:如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE,交⊙O于D.
已知:如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE,交⊙O于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com