已知关于x的方程4x2-2(m+1)x+m=0的两根恰是某直角三角形两锐角的正弦,求m的值.
解:由x的方程4x
2-2(m+1)x+m=0的两根恰是某直角三角形两锐角的正弦,
设两根为:sinα,sinβ,则sinα+sinβ=

,sinαsinβ=

,
∵α+β=90°,∴sinα=cosβ,代入得:cosβ+sinβ=

,cosβsinβ=

,
∴1+2cosβsinβ=1+

=
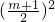
,解得:m
2=3,
又∵cosβsinβ=

>0,∴m>0,
故m=

.
分析:由x的方程4x
2-2(m+1)x+m=0的两根恰是某直角三角形两锐角的正弦,设两根为:sinα,sinβ,根据韦达定理列出方程后求解.
点评:本题考查了根与系数的关系及互余两角三角函数的关系,难度不大,关键是巧妙运用(sinα)
2+(cosα)
2=1进行解题.

 ,sinαsinβ=
,sinαsinβ= ,
, ,cosβsinβ=
,cosβsinβ= ,
, =
=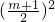 ,解得:m2=3,
,解得:m2=3, >0,∴m>0,
>0,∴m>0, .
.
