
如图,E是矩形ABCE的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H。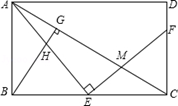
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=2,求EM的长。
(1)可证明△ABE中,△ECF∠ABE=∠ECF,∠BAE=∠CEF,所以△ABE∽△ECF
(2)△ABH∽△ECM:由BG⊥AC可得∠ABG+∠BAG=90°,则有∠ABH=∠ECM,又∠BAH=∠CEM。
(3)
解析试题分析:(1)由四边形ABCD是矩形,可得∠ABE=∠ECF=90°,由AE⊥EF,∠AEB+∠FEC=90°,可得∠BAE=∠CEF,即可证得△ABE∽△ECF.
(2)由BG⊥AC可得∠ABG+∠BAG=90°,则有∠ABH=∠ECM,又∠BAH=∠CEM,
则可证得△ABH∽△ECM.
(3)作MR⊥BC,垂足为R,由AB=BE=EC=2,
因为AB∥MR。则可证明Rt△ABC∽Rt△MRC。所以CR=2MR
且AB:BC=MR:RC=1:2,且∠AEB=45°,则通过平角性质可得∠MER=90°-∠AEB=45°,从而可得MR=ER= RC=
RC= ,所以EM=
,所以EM= .
.
考点:相似三角形性质与判定
点评:本题难度中等,主要考查学生对相似三角形性质与判定知识点的掌握。为中考常考题型,要求学生培养数形结合思想,运用到考试中去。


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
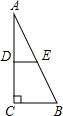 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
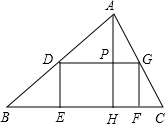
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初二数学 华东师大(新课标2001-3年初审) 华东师大(新课标2001-3年初审) 题型:044
如图,BO是Rt△ABC斜边上的中线,延长BO至点D,使DO=BO,连结AD,CD,则四边形ABCD是矩形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东揭阳揭西张武帮中学九年级上质检考试数学试卷B(解析版) 题型:选择题
如图,AC.BD是矩形ABCD的对角线,过点D作DF∥AC交BC的延长线于F,则图中与△ABC全等的三角形共有( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com