
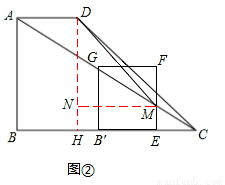
已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.
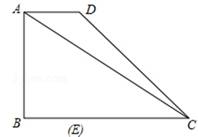
(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFG为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM.是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
(1)2;(2)存在,t=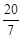 或﹣3+
或﹣3+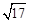 ;
;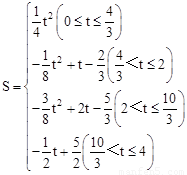 .
.
【解析】
试题分析:(1)首先设正方形BEFG的边长为x,易得△AGF∽△ABC,根据相似三角形的对应边成比例,即可求得BE的长;(2)首先由△MEC∽△ABC与勾股定理,求得B′M,DM与B′D的平方,然后分别从若∠DB′M、∠DB′M和∠B′DM分别是直角,列方程求解即可;(3)分别从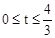 ,
,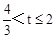 ,
,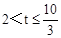 和
和 时去分析求解即可求得答案:
时去分析求解即可求得答案:
①如图③,当F在CD上时,EF:DH=CE:CH,即2:3=CE:4,∴CE=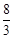 .
.
∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣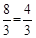 .
.
∵ME=2﹣ t,∴FM=
t,∴FM= t,
t,
∴当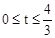 时,S=S△FMN=
时,S=S△FMN= ×t×
×t× t=
t=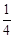 t2.
t2.
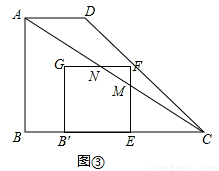
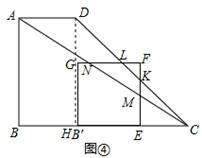
②如图④,当G在AC上时,t=2,
∵EK=EC•tan∠DCB= 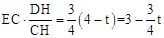 ,∴FK=2﹣EK=
,∴FK=2﹣EK=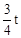 ﹣1.
﹣1.
∵NL=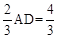 ,∴FL=t﹣
,∴FL=t﹣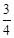 ,∴当
,∴当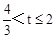 时,S=S△FMN﹣S△FKL=
时,S=S△FMN﹣S△FKL=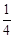 t2﹣
t2﹣ (t﹣
(t﹣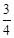 )(
)(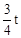 ﹣1)=
﹣1)=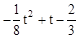 .
.
③如图⑤,当G在CD上时,B′C:CH=B′G:DH,即B′C:4=2:3,解得:B′C=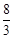 ,
,
∴EC=4﹣t=B′C﹣2=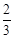 .
∴t=
.
∴t=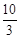 .
.
∵B′N= B′C=
B′C= (6﹣t)=3﹣
(6﹣t)=3﹣ t,∴GN=GB′﹣B′N=
t,∴GN=GB′﹣B′N= t﹣1.
t﹣1.
∴当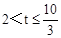 时,S=S梯形GNMF﹣S△FKL=
时,S=S梯形GNMF﹣S△FKL= ×2×(
×2×( t﹣1+
t﹣1+ t)﹣
t)﹣ (t﹣
(t﹣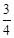 )(
)(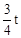 ﹣1)=
﹣1)=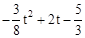 .
.
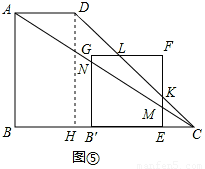
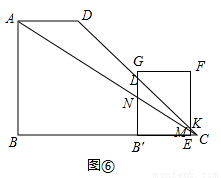
④如图⑥,当 时,
时,
∵B′L=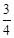 B′C=
B′C=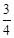 (6﹣t),EK=
(6﹣t),EK=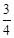 EC=
EC=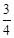 (4﹣t),B′N=
(4﹣t),B′N= B′C=
B′C= (6﹣t)EM=
(6﹣t)EM= EC=
EC= (4﹣t),
(4﹣t),
∴S=S梯形MNLK=S梯形B′EKL﹣S梯形B′EMN=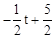 .
.
综上所述: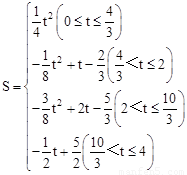 .
.
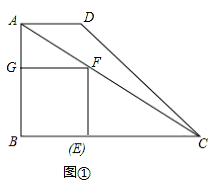
试题解析:(1)如图①,设正方形BEFG的边长为x,则BE=FG=BG=x.
∵AB=3,BC=6,∴AG=AB﹣BG=3﹣x.
∵GF∥BE,∴△AGF∽△ABC. ∴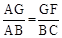 ,即
,即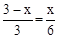 ,解得:x=2,即BE=2.
,解得:x=2,即BE=2.
(2)存在满足条件的t,理由如下:
如图②,过点D作DH⊥BC于H,则BH=AD=2,DH=AB=3,
由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t,
∵EF∥AB,∴△MEC∽△ABC. ∴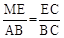 ,即
,即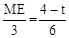 . ∴ME=2﹣
. ∴ME=2﹣ t.
t.
在Rt△B′ME中,B′M2=ME2+B′E2=22+(2﹣ t)2=
t)2=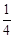 t2﹣2t+8.
t2﹣2t+8.
在Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13.
过点M作MN⊥DH于N,则MN=HE=t,NH=ME=2﹣ t,∴DN=DH﹣NH=3﹣(2﹣
t,∴DN=DH﹣NH=3﹣(2﹣ t)=
t)= t+1.
t+1.
在Rt△DMN中,DM2=DN2+MN2=( t+1)2+ t 2=
t+1)2+ t 2=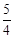 t2+t+1.
t2+t+1.
(Ⅰ)若∠DB′M=90°,则DM2=B′M2+B′D2,即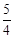 t2+t+1=(
t2+t+1=(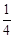 t2﹣2t+8)+(t2﹣4t+13),解得:t=
t2﹣2t+8)+(t2﹣4t+13),解得:t=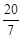 .
.
(Ⅱ)若∠B′MD=90°,则B′D2=B′M2+DM2,即t2﹣4t+13=(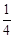 t2﹣2t+8)+(
t2﹣2t+8)+(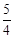 t2+t+1),解得:t1=﹣3+
t2+t+1),解得:t1=﹣3+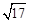 ,t2=﹣3﹣
,t2=﹣3﹣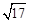 (舍去).∴t=﹣3+
(舍去).∴t=﹣3+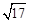 .
.
(Ⅲ)若∠B′DM=90°,则B′M2=B′D2+DM2,即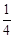 t2﹣2t+8=(t2﹣4t+13)+(
t2﹣2t+8=(t2﹣4t+13)+(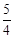 t2+t+1),此方程无解.
t2+t+1),此方程无解.
综上所述,当t=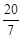 或﹣3+
或﹣3+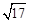 时,△B′DM是直角三角形.
时,△B′DM是直角三角形.
(3)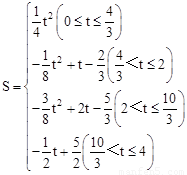 .
.
考点:1.相似三角形的判定和性质;2.勾股定理和逆定理;3.正方形的性质;4.直角梯形的性质;5.平移的性质;6.分类思想的应用.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源:2011年河南省周口市初一下学期相交线与平行线专项训练 题型:解答题
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,建立平面直角坐标系.已知OA=4,OB=3,一动点P从O出发沿OA方向,以每秒1个
单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动.当Q到达B时,P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t>0).
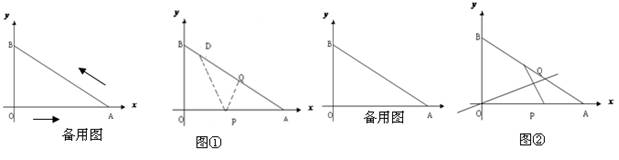
(1) 试求出△APQ的面积S与运动时间t之间的函数关系式;
(2) 在某一时刻将△APQ沿着PQ翻折,使得点A恰好落在AB边的点D处,如图①.
求出此时△APQ的面积.
(3) 在点P从O向A运动的过程中,在y轴上是否存在着点E使得四边形PQBE为等腰梯
形?若存在,求出点E的坐标;若不存在,请说明理由.
(4) 伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F. 当DF经过原点O时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源:2011年河南省周口市初一下学期平移专项训练 题型:解答题
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,建立平面直角坐标系.已知OA=4,OB=3,一动点P从O出发沿OA方向,以每秒1个
单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动.当Q到达B时,P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t>0).

(1) 试求出△APQ的面积S与运动时间t之间的函数关系式;
(2) 在某一时刻将△APQ沿着PQ翻折,使得点A恰好落在AB边的点D处,如图①.
求出此时△APQ的面积.
(3) 在点P从O向A运动的过程中,在y轴上是否存在着点E使得四边形PQBE为等腰梯
形?若存在,求出点E的坐标;若不存在,请说明理由.
(4) 伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F. 当DF经过原点O时,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com