
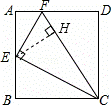
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
①∠AEF=∠BCE;
②AF+BC>CF;
③S△CEF=S△EAF+S△CBE;
④若 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.
其中正确的结论是 .(填写所有正确结论的序号)

①③④
解:∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠BEC+∠BCE=90°,
∴∠AEF=∠BCE,故①正确;
又∵∠A=∠B=90°,
∴△AEF∽△BCE,
∴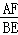 =
=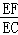 ,
,
∵点E是AB的中点,
∴AE=BE,
∴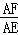 =
=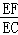 ,
,
又∵∠A=∠CEF=90°,
∴△AEF∽△ECF,
∴∠AFE=∠EFC,
过点E作EH⊥FC于H,
则AE=DH,
在△AEF和△HEF中,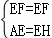 ,
,
∴△AEF≌△HEF(HL),
∴AF=FH,
同理可得△BCE≌△HCE,
∴BC=CH,
∴AF+BC=CF,故②错误;
∵ △AEF≌△HEF,△BCE≌△HCE,
△AEF≌△HEF,△BCE≌△HCE,
∴S△ CEF=S△EAF+S△CBE,故③正确;
CEF=S△EAF+S△CBE,故③正确;
若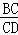 =
=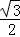 ,则cot∠BCE=
,则cot∠BCE=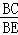 =
=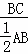 =
=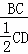 =
=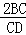 =2×
=2×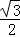 =
=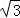 ,
,
∴∠BCE=30°,
∴∠DCF=∠ECF=30°,
在△CEF和△CDF中,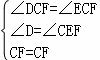 ,
,
∴△CEF≌△CDF(AAS),故④正确,
综上所述,正确的结论是①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
|
| A. | y=3(x+1)2+2 | B. | y=3(x+1)2﹣2 | C. | y=3(x﹣1)2+2 | D. | y=3(x﹣1)2﹣2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动.设运动时间为t秒(t>0).
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
( 3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF=
3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF= S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列调查适合用全面调查方式的是(  )
)
| A.了解黑龙江省居民年人均收入 | B.了解北京市中小学生的近视率 |
| C.调查2014年足球世界杯的收视率 | D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com