Question

等腰三角形的腰长等于2cm，面积等于1cm²时，则它的顶角等于度．

1. A.
   150
2. B.
   30
3. C.
   60
4. D.
   150或30

Answer 1

D
分析：做腰上的高，根据三角形的面积公式可求得高的长，根据直角三角形的性质不难求解．
解答：①过点C作CD⊥AB，
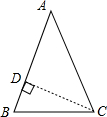
∵AB=AC=2cm，S_△ABC=1cm²，
∴S△ABC=×AB×CD，
∴CD=1cm，
∴∠A=30°．
②过点C作CD⊥AB，交BA的延长线与点D．
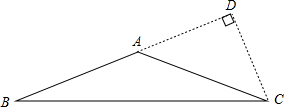
∵AB=AC=2cm，S_△ABC=1cm²，
∴S△ABC=×AB×CD，
∴CD=1cm，
∴∠DAC=30°，
∴∠BAC=150°
综上可得顶角为30°或150°．
故选D．
点评：此题考查了勾股定理及等腰三角形的性质，还涉及了三角形的面积公式，正弦三角函数与边长之间的关系，难点在于需要分类讨论，容易造成漏解．