
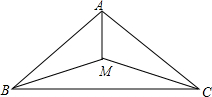
 如图,在△ABC中,BM=MC,∠ABM=∠ACM,求证:AM平分∠BAC.
如图,在△ABC中,BM=MC,∠ABM=∠ACM,求证:AM平分∠BAC. 分析 由条件BM=MC就可以得出∠MBC=∠MCB,由等式的性质就可以得出∠ABC=∠ACB,就有AB=AC,再证明△AMB≌△AMC就可以得出结论.
解答 证明:∵BM=MC,
∴∠MBC=∠MCB.
∵∠ABM=∠ACM,
∴∠MBC+∠ABM=∠MCB+∠ACM,
∴∠ABC=∠ACB,
∴AB=AC.
在△AMB和△AMC中,
$\left\{\begin{array}{l}{AB=AC}\\{BM=CM}\\{AM=AM}\end{array}\right.$,
∴△AMB≌△AMC(SSS),
∴∠BAM=∠CAM,
∴AM平分∠BAC.
点评 本题考查了等腰三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,角平分线的判定的运用,解答时证明三角形全等是关键.


 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
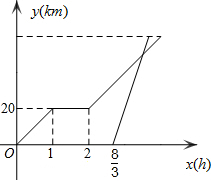 暑假期间,小亮骑自行车从家里出去旅游,从家出发一小时后到达甲地,游玩一段时间后,按元素前往乙地,小亮离家2小时40分钟后,爸爸驾车沿相同录像前往乙地,如图是他们离家的路程y(km)与小亮离家时间x(h)的函数图象,已知爸爸驾车的速度是小亮骑车速度的3倍.
暑假期间,小亮骑自行车从家里出去旅游,从家出发一小时后到达甲地,游玩一段时间后,按元素前往乙地,小亮离家2小时40分钟后,爸爸驾车沿相同录像前往乙地,如图是他们离家的路程y(km)与小亮离家时间x(h)的函数图象,已知爸爸驾车的速度是小亮骑车速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com