练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．化简$\frac{2}{x+1}$-$\frac{x-2}{{x}^{2}-1}$的结果是$\frac{x}{{x}^{2}-1}$．

    分析 原式两项通分并利用同分母分式的减法法则计算即可得到结果．

    解答 解：原式=$\frac{2（x-1）}{（x+1）（x-1）}$-$\frac{x-2}{（x+1）（x-1）}$
    =$\frac{2x-2-x+2}{（x+1）（x-1）}$
    =$\frac{x}{{x}^{2}-1}$．
    故答案为：$\frac{x}{{x}^{2}-1}$．

    点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．如图，数轴上有A、B、C、D四点，根据图中各点的位置，判断与10-2$\sqrt{39}$最接近的点是（　　）
    A．AB．BC．CD．D

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于点D，连接CD，则阴影部分的面积为（　　）
    A．π-1B．2π-1C．$\frac{1}{2}$π-1D．$\frac{1}{2}$π-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．从地面竖直向上抛出一小球，小球的高度h（米）与小球运动时间t（秒）的关系式是h=30t-5t2，小球运动中的最大高度是45米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

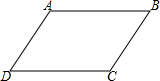    10．（1）∵∠A+∠B=180°（已知）
    ∴AD∥BC（同旁内角互补，两直线平行）
    （2）∵∠A+∠D=180°（已知）
    ∴AB∥CD（同旁内角互补，两直线平行）
    小结：判定两条直线平行的方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，⊙O是△ABC的内切圆，点D、E、F为切点，点M为优弧DEF上任意一点，∠B=66°，∠C=37°，求∠M的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

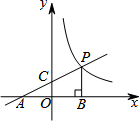    7．如图，直线y1=$\frac{1}{2}$x+1分别交x轴，y轴于点A，C，点P是直线AC与双曲线y2=$\frac{k}{x}$（x＞0）在第一象限内的交点，PB⊥x轴于点B，△PAB的面积为4．
    （1）求双曲线的解析式；
    （2）根据图象直接写出y1＜y2的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某公司投资1200万元购买了一条新生产线生产新产品．根据市场调研，生产每件产品需要成本50元，该产品进入市场后不得低于80元/件且不得超过160元/件，该产品销售量y（万件）与产品售价x（元）之间的关系如图所示．
    （1）求y与x之间的函数关系式，并写出x的取值范围；
    （2）第一年公司是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；
    （3）在（2）的前提下，即在第一年盈利最大或者亏损最小时，公司第二年重新确定产品售价，能否使前两年盈利总额达790万元？若能，求出第二年产品售价；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，点P、D分别在AO和BC上，PB=PD，DE⊥AC于点E．
    （1）若PB平分∠ABO，求证：AP=CD；
    （2）若点P是一个动点，点P运动到OC的中点P′时，满足题中条件的点D也随之在直线BC上运动到点D′，请直接写出CD′与AP′的数量关系．（不必写解答过程）

    查看答案和解析>>

    同步练习册答案