
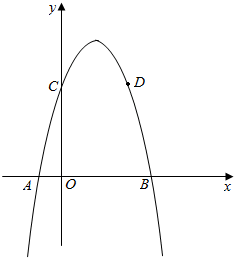
 已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.
已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.分析 (1)由对称性得点C的坐标和对称轴为x=2,求出b和c,写出抛物线解析式;
(2)先求直线BC的解析式:y=-x+5,根据点M的坐标发现,点M所在的直线y=-x+2与直线BC平行,且过对称轴与x轴的交点H,利用两三角形全等列方程组求解;
(3)先判断出点F既在直线BC上又在抛物线对称轴上,从而得出∠EKF=$\frac{1}{2}$∠ENF,判断出点E,F,K在以点N为圆心3为半径的圆上,最后进行计算即可.
解答 解:(1)∵点C在y轴上,点D为(4,5),且C、D两点关于抛物线的对称轴对称,
∴C(0,5),
∴抛物线的对称轴为x=-$\frac{b}{-1×2}$=2,
∴b=4.
∴抛物线的解析式为y=-x2+4x+5.
(2)令y=-x2+4x+5中y=0,则-x2+4x+5=-(x+1)(x-5)=0,
解得:x=-1,或x=5,
∴点A的坐标为(-1,0),点B的坐标为(5,0).
设直线BC的解析式为y=kx+5,
∴0=5k+5,解得k=-1,
∴直线BC的解析式为y=-x+5,
设点E的坐标为(a,-a2+4a+5),点F的坐标为(n,-n+5),
如图1,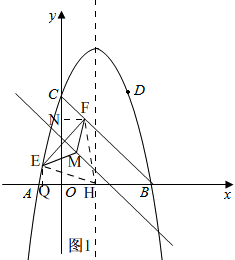
分别过E和F向两坐标轴作垂线,垂足分别为Q、N,交抛物线对称轴为G,设抛物线对称轴与x轴交于点H,
∵点M(m,-m+2)
∴MH∥BC且直线MH的解析式为:y=-x+2
∵ME=MF
∴EH=FH
得△FGH≌△EGH
∴EQ=FH,QH=GH
则 $\left\{\begin{array}{l}{2-n=-{a}^{2}+4a+5}\\{-n+5=-a+2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=6}\\{{n}_{1}=9}\end{array}\right.$,$\left\{\begin{array}{l}{{a}_{2}=-1}\\{{n}_{2}=2}\end{array}\right.$.
当a=6时,-a2+4a+5=-7,
∴E(6,-7)
当a=-1时,-a2+4a+5=0
∴E(-1,0)
∴E(6,-7)或E(-1,0),
(3)由(1)有,抛物线的对称轴为x=2,
∵点E在对称轴的左侧,
∴E(-1,0),即点E与点A重合,
由(2)有,F(2,3),
∵抛物线的对称轴为x=2,
∴点F在抛物线的对称轴上,
∴NF=NE=3,
∴∠ENF=90°,
∵∠EKF=45°,
∴∠EKF=$\frac{1}{2}$∠ENF,
又∵NF=NE=3,
∴点K必在以点N为圆心,3为半径圆上,
∴NK=3,
如图2所示,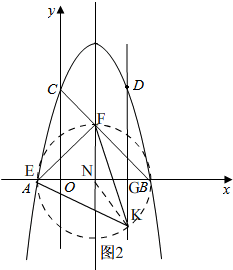
∵点K在过点D且与y轴平行的直线上,D(4,5),
∴K点的横坐标为4,
连接NK,
在Rt△NGK中,NG=OG-ON=4-2=2,NK=3,
∴GK=$\sqrt{N{K}^{2}-N{G}^{2}}$=$\sqrt{5}$,
∵∠EKF=45°,
∴K(4,-$\sqrt{5}$),
假设存在点M满足ME=MK,
∵ME=MF,
∴ME=MF=MK,
∴点M是△EFK的外接圆的圆心,
∴点M和点N重合,
∵点N在抛物线的对称轴x=2上,
∴点M在抛物线的对称轴上,M(2,0)
即:存在点M满足ME=MK,并且在抛物线的对称轴上.
点评 此题是二次函数综合题,考查了待定系数法求抛物线和直线的解析式,抛物线对称轴的确定,三角形全等的判定和性质,函数图象的交点坐标的确定等知识点.解本题的关键用方程的思想求出点的坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 节水量(单位:吨) | 0.5 | 1 | 1.5 | 2 |
| 家庭数(户) | 2 | 3 | 4 | 1 |
| A. | 240吨 | B. | 360吨 | C. | 180吨 | D. | 200吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
| 不超过150千瓦时的部分 | 0.6 |
| 超过150千瓦时,但不超过300千瓦时的部分 | 0.65 |
| 超过300千瓦时的部分 | 0.9 |
| 某居民一个月用电量(千瓦时) | 100 | 150 | 200 | 300 | 350 | 400 | … |
| 电费价格(元) | 60 | 90 | 122.5 | 187.5 | 232.5 | 277.5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com