
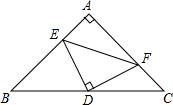
 如图,在等腰Rt△ABC中,D是斜边BC的中点,E在边AB上,F在边AC上,且∠EDF=90°.
如图,在等腰Rt△ABC中,D是斜边BC的中点,E在边AB上,F在边AC上,且∠EDF=90°.| 2 |
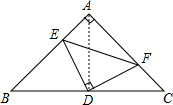 解:(1)连接AD.
解:(1)连接AD.| DE2+DF2 |
| 2 |


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
 实验探究:为发挥广大读者艺术特长,我报《数学专页》于2006年1月份举办了一次栏标设计大赛,截至4月份大赛已圆满结束.本次比赛收到了近千幅设计作品,其中一幅参赛作品如图.
实验探究:为发挥广大读者艺术特长,我报《数学专页》于2006年1月份举办了一次栏标设计大赛,截至4月份大赛已圆满结束.本次比赛收到了近千幅设计作品,其中一幅参赛作品如图.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com