
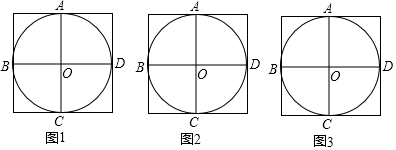
分析 ①如图1中,∠P即为所求;
②如图2中,∠P即为所求;
③如图3中,∠EPC即为所求;
解答 解:①如图1中,tan∠P=1.
理由:∵∠P=$\frac{1}{2}$∠DOC=45°,
∴tan∠P=1.
∴∠P即为所求;
如图2中,tan∠P=$\frac{1}{2}$.
理由:∵∠P=∠FAC,
∴tan∠P=tan∠FAC=$\frac{FC}{AC}$=$\frac{1}{2}$.
∴∠P即为所求.
如图3中,tan∠EPC=2.
理由:∵∠E=∠FAC,PE是直径,
∴∠FAC+∠AFC=90°,∠E+∠EPC=90°,
∴∠AFC=∠EPC,tan∠EPC=tan∠AFC=$\frac{AC}{CF}$=2.
∴∠EPC即为所求;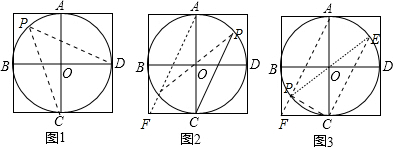
点评 此题考查了圆周角定理与三角函数的性质.此题难度不大,注意掌握数形结合思想与转化思想的应用.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 2分 | B. | 4分 | C. | 6分 | D. | 8分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
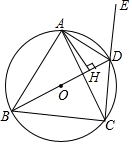 如图,BD是⊙O的直径,四边形ABCD是⊙O的内接四边形,且AB=AC,AH⊥BD于点H,延长CD至点E.
如图,BD是⊙O的直径,四边形ABCD是⊙O的内接四边形,且AB=AC,AH⊥BD于点H,延长CD至点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.744×106亿元 | B. | 7.44×105亿元 | C. | 74.4×104亿元 | D. | 744×103亿元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
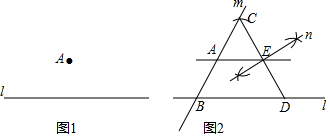
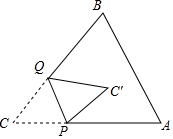 如图,△ABC,∠C=45°,点P、Q分别在射线CA、CB上,且CP=2,将△ABC沿PQ折叠,点C落在平面上点C′处.
如图,△ABC,∠C=45°,点P、Q分别在射线CA、CB上,且CP=2,将△ABC沿PQ折叠,点C落在平面上点C′处.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥3且x≠-1 | B. | x>3且x≠-1 | C. | x>-1 | D. | x≥3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com