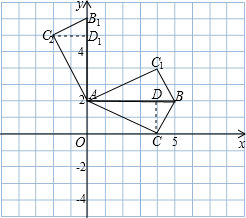
解:(1)作CD⊥AB交AB于点D;
由△ACD∽△BCD得到BD=1,所以AB=5,
又因为AB∥x轴,
所以点B的坐标为(5,2)
设函数解析式为:y=ax
2+bx+c,把A,B,C三点代入得:
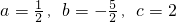
所以

;
(2)作C
2D
1⊥AB
1;
由△ACD≌△AC
2D
1得:
C
2D
1=2,AD
1=4,
所以C
2(-2,6)
把x=-2代入得y=9,
所以点C
2不在抛物线上;
(3)由题(1)可知

,
所以顶点坐标为
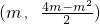
;
直线AC的解析式为
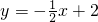
,把x=m代入
得

,
直线BC的解析式为y=2x-8,把x=m代入
得y=2m-8,
因为顶点在三角形内部或者边上,
所以0≤m≤5,
①
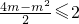
,解得m可以取任意实数;
②
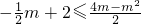
,解得1≤m≤4(可以图象法解);
③
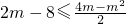
,解得-4≤m≤4;
得出其中任意2个不等式给,4个
所以m的取值范围是1≤m≤4.
分析:(1)过C作CD⊥AB于D,根据A、C的坐标,易求得AD、CD的长,在Rt△ACB中,CD⊥AB,利用射影定理可求得BD的长(也可利用相似三角形得到),由此求得点B的坐标,进而可利用待定系数法求得抛物线的解析式;
(2)根据△ABC的两次旋转变化可知AB
1落在y轴上,可过C
2作C
2D
1⊥AB
1,根据△ACD≌△AC
2D
1得AD
1、CD
1的长,从而求出点C
2的坐标,然后将其代入抛物线的解析式中进行验证即可;
(3)在(1)题中求得了抛物线的二次项系数,即可用m表示出平移后的抛物线顶点坐标,得
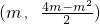
,由于此顶点在△ACB的边上或内部,因此顶点横坐标必在0≤m≤5的范围内,然后分三种情况考虑:
①顶点纵坐标应小于或等于A、B的纵坐标.
②求出直线AC和直线x=m的交点纵坐标,那么顶点纵坐标应该大于等于此交点纵坐标.
③求出直线BC和直线x=m的交点纵坐标,方法同②.
结合上面四个不等关系式,即可得到m的取值范围.
点评:此题主要考查了图形旋转变化、相似及全等三角形的判定和性质、二次函数解析式的确定以及函数图象的平移,同时还涉及到简单线性规划的实际应用,难度较大.

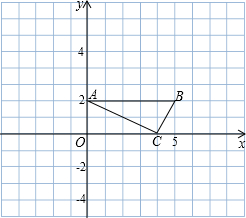 在平面直角坐标系中点A(0,2)C(4,0),AB∥x轴,△ABC是直角三角形,∠ACB=90°.
在平面直角坐标系中点A(0,2)C(4,0),AB∥x轴,△ABC是直角三角形,∠ACB=90°. 解:(1)作CD⊥AB交AB于点D;
解:(1)作CD⊥AB交AB于点D;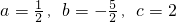
 ;
; ,
,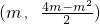 ;
;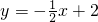 ,把x=m代入
,把x=m代入 ,
,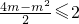 ,解得m可以取任意实数;
,解得m可以取任意实数;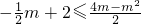 ,解得1≤m≤4(可以图象法解);
,解得1≤m≤4(可以图象法解);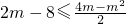 ,解得-4≤m≤4;
,解得-4≤m≤4;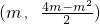 ,由于此顶点在△ACB的边上或内部,因此顶点横坐标必在0≤m≤5的范围内,然后分三种情况考虑:
,由于此顶点在△ACB的边上或内部,因此顶点横坐标必在0≤m≤5的范围内,然后分三种情况考虑:

 阅读快车系列答案
阅读快车系列答案 在平面直角坐标系中点A(0,2)C(4,0),AB∥x轴,△ABC是直角三角形,∠ACB=90°.
在平面直角坐标系中点A(0,2)C(4,0),AB∥x轴,△ABC是直角三角形,∠ACB=90°.