
 如图,已知∠A,请你仅用尺规,按下列要求作图和计算(不必写画法):
如图,已知∠A,请你仅用尺规,按下列要求作图和计算(不必写画法):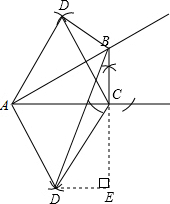 解:(1)如图所示,△ABC为所求作的直角三角形(答案不唯一);
解:(1)如图所示,△ABC为所求作的直角三角形(答案不唯一); =
=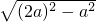 =
= a,
a, AC=
AC= a,CE=
a,CE= a•sin60°=
a•sin60°= a×
a× =
= a,
a, a=
a= a,
a, =
=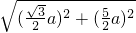 =
= a;
a; a或a.
a或a. a或a.
a或a.

科目:初中数学 来源: 题型:
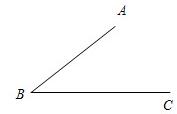 23、如图,已知∠ABC.请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边与点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
23、如图,已知∠ABC.请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边与点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
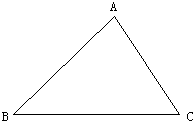 20、如图,已知△ABC,请你按要求用尺规作出下列图形(不写作法,但要保留作图痕迹).
20、如图,已知△ABC,请你按要求用尺规作出下列图形(不写作法,但要保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:
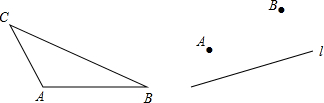
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com