练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图，点P为等腰梯形ABCD上底AD上一动点，连接PB，PC，点E、F、G分别为PB、PC、BC的中点．当点P运动到什么位置时，四边形PEGF为菱形？

    解：当点P运动到AD中点时，四边形PEGF为菱形，
    ∵点E、F、G分别为PB、PC、BC的中点，
    ∴EG、FG分别是△BPC的中位线，
    ∴EG∥PF，FG∥PB，EG=PC，FG=BP，
    ∴四边形PEGF是平行四边形，
    又∵点P是AD中点，四边形ABCD是等腰梯形，
    ∴BP=CP，
    ∴EG=FG，
    ∴四边形PEGF为菱形．
    分析：根据一组邻边相等的平行四边形是菱形，所以只要EP=FP就可以，即BP=CP，所以点P是AD的中点．
    点评：本题考查了等腰梯形的性质及菱形的判定，解答本题的关键是掌握菱形的判定定理及三角形中位线的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    25、已知：如图，点C为线段AB上一点，△ACM、△CBN是等边三角形，可以说明：△ACN≌△MCB，从而得到结论：AN=BM．
    现要求：
    （1）将△ACM绕C点按逆时针方向旋转180°，使A点落在CB上．请对照原题图在下图中画出符合要求的图形（不写作法，保留作图痕迹）；
    （2）在（1）所得到的图形中，结论“AN=BM”是否还成立？若成立，请给予证明；若不成立，请说明理由；
    （3）在（1）所得到的图形中，设MA的延长线与BN相交于D点，请你判断△ABD与四边形MDNC的形状，并说明你的结论的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

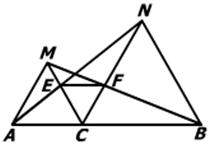
    27、已知：如图，点C为线段AB上一点，△ACM，△CBN都是等边三角形，AN交MC于点E，BM交CN于点F．
    （1）求证：AN=BM；
    （2）求证：△CEF为等边三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图①，点C为线段AB上一点，△ACM和△CBN都是等边三角形，AN，BM交于点P，则△BCM≌△NCA，易证结论：①BM=AN．
    （1）请写出除①外的两个结论：②
    ∠MBC=∠ANC
    ∠MBC=∠ANC
    ；③
    ∠BMC=∠NAC
    ∠BMC=∠NAC
    ．
    （2）将△ACM绕点C顺时针方向旋转180°，使点A落在BC上．请对照原题图形在图②画出符合要求的图形．（不写作法，保留作图痕迹）
    （3）在（2）所得到的下图②中，探究“AN=BM”这一结论是否成立．若成立，请证明：若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，点C为线段AB上一点，△ACM, △CBN都是等边三角形，AN交MC于点E，BM交CN于点F.

    (1)求证：AN=BM;
    (2)求证：△CEF为等边三角形

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（广东深圳） 题型：解答题

    已知：如图，点C为线段AB上一点，△ACM, △CBN都是等边三角形，AN交MC于点E，BM交CN于点F.

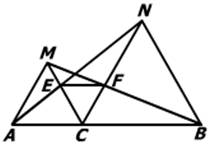
    (1)求证：AN=BM;

    (2)求证：△CEF为等边三角形

     

    查看答案和解析>>

    同步练习册答案