练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图：P是?ABCD内的一点，S△APB：S△ABCD=1：3，则S△CPD：S△ABCD=1：6．

    分析 根据平行四边形的面积和三角形的面积可得S△ABP+S△CDP=S△ADP+S△BCP=$\frac{1}{2}$S?ABCD，然后再由条件S△APB：S△ABCD=1：3可得答案．

    解答 解：由题意可得，S△ABP+S△CDP=S△ADP+S△BCP=$\frac{1}{2}$S?ABCD，
    ∵S△APB：S?ABCD=1：3，
    ∴$\frac{{S}_{△ABP}}{{S}_{平行四边形ABCD}}$=$\frac{1}{3}$，
    ∴$\frac{{S}_{平行四边形ABCD}-{S}_{△PCD}}{{S}_{平行四边形ABCD}}$=$\frac{1}{3}$，
    ∴S△CPD：S?ABCD=1：6，
    故答案为：1：6．

    点评 本题主要考查平行四边形的性质及三角形的面积问题，应熟练掌握平行四边形的性质，能够求解一些简单的计算问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．分解因式
    （1）4x2-36；
    （2）-4m3+8m2+32m；
    （3）（y2-1）2-6（y2-1）+9；
    （4）a2+ac-bc-b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，甲、乙、丙、丁四个扇形的面积之比是1：2：3：4，则甲、乙、丙、丁四个扇形中圆心角度数最大的是（　　）度．
    A．36B．72C．144D．156

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：$\frac{1}{1-a}$+$\frac{1}{1+a}$+$\frac{2}{1+{a}^{2}}$+$\frac{4}{1+{a}^{4}}$-$\frac{8}{1-{a}^{8}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

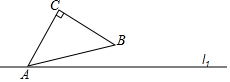    15．点c是直线l1外一定点，点A是直线l1上一动点，以AC为腰作等腰直角三角形ABC（点B在点C的右侧），当点A在直线l1上运动时，请画出点B的轨迹．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若m2x2-2x+n2是一个完全平方式，则mn=±1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，已知函数y=-2x+4的图象，观察图象回答下列问题：
    （1）x＜2时，y＞0；（2）x＞2时，y＜0；
    （3）x=2时，y=0；（4）x＜0时，y＞4；
    （5）当0＜x＜1时，函数y的取值范围是2＜y＜4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．图①是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，拱顶距离桥面$\frac{1}{2}$m．水面AB宽4m．如图②以桥面为x轴，与水面AB中点垂直的直线为y轴建立平面直角坐标系．
    （1）写出点A的坐标；
    （2）求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知关于x的方程x2+$\frac{1}{{x}^{2}}$+2（x+$\frac{1}{x}$）=6，那么x+$\frac{1}{x}$的值为-4或2．．

    查看答案和解析>>

    同步练习册答案