Question

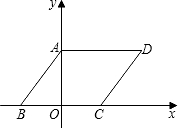
平行四边形ABCD在平面直角坐标系中的位置如图所示，其中A（﹣4，0），B（2，0），C（3，3）反比例函数的图象经过点C．

（1）求此反比例函数的解析式；

（2）将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B，请你通过计算说明点D′在双曲线上；

（3）请你画出△AD′C，并求出它的面积．

 

Answer 1

【答案】

解：（1）∵点C（3，3）在反比例函数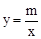的图象上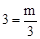，∴。∴m=9。

∴反比例函数的解析式为。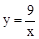

（2）过C作CE⊥x轴于点E，过D作DF⊥x轴于点F，则△CBE≌△DAF，

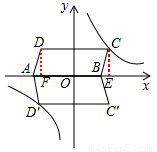
∴AF=BE，DF=CE。

∵A（﹣4，0），B（2，0），C（3，3），

∴DF=CE=3，OA=4，OE=3，OB=2。

∴。

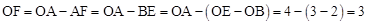∴D（﹣3，3）。

∵点D′与点D关于x轴对称，∴D′（﹣3，﹣3）。

把x=﹣3代入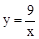得，y=﹣3，∴点D′在双曲线上。

（3）作图如下：

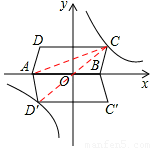
∵C（3，3），D′（﹣3，﹣3），∴点C和点D′关于原点O中心对称。

∴D′O=CO=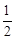D′C。

∴S_△AD′C=2S_△AOC=2×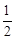AO•CE=2×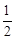×4×3=12。

【解析】

试题分析：（1）把点C（3，3）代入反比例函数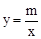，求出m，即可求出解析式。

（2）过C作CE⊥x轴于点E，过D作DF⊥x轴于点F，则△CBE≌△DAF，根据线段之间的数量关系进一步求出点D的坐标，再点D′与点D关于x轴对称，求出D′坐标，进而判断点D′是不是在双曲线。

（3）根据C（3，3），D′（﹣3，﹣3）得到点C和点D′关于原点O中心对称，进一步得出D′O=CO=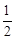D′C，由S_△AD′C=2S_△AOC=2×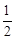AO•CE求出面积的值。