
分析 把解代入方程组得到关于m、n的方程组、消去n得到关于m的方程(3m-4)(7m-12)=4.由m是整数可得3m-4和7m-12都是4的约数,由此可得到m的范围,从而得到m、n的值.
解答 解:将$\left\{\begin{array}{l}{x=2}\\{y=\frac{1}{2}}\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}{4m+\frac{1}{4}n=6}\\{2{m}^{2}-\frac{1}{2}{n}^{2}+24=0}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{16m+n=24}&{①}\\{4{m}^{2}-{n}^{2}=-48}&{②}\end{array}\right.$,
由①得:n=24-16m,代入②得
4m2-(24-16m)2=-48,
即(16m-24)2-(2m)2=48,
∴(16m-24+2m)(16m-24-2m)=48,
整理得(3m-4)(7m-12)=4.
∵m是整数,
∴3m-4和7m-12都是整数,且都是4的约数,
∴-4≤3m-4≤4,且-4≤7m-12≤4,
∴0≤m≤$\frac{8}{3}$,且$\frac{8}{7}$≤m≤$\frac{16}{7}$,
∴m=2.此时(3m-4)(7m-12)=4,
n=24-16×2=-8.
∴m的值为2,n的值为-8.
点评 本题主要考查了解高次方程组、因式分解、整除问题等知识,有一定的难度,运用消元法和因式分解法得到(3m-4)(7m-12)=4是解决本题的关键.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
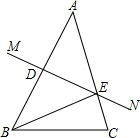 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.
如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCE的周长等于25cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48 | B. | 50 | C. | 66 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -8-3=-5 | B. | $(-\frac{1}{3})×3÷3×(-\frac{1}{3})=1$ | C. | 7a+a=7a2 | D. | 4xy2-2xy2=2xy2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
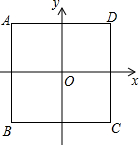 如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com