设A是给定的正有理数.
(1)若A是一个三边长都是有理数的直角三角形的面积,证明:一定存在3个正有理数x、y、z,使得x2-y2=y2-z2=A.
(2)若存在3个正有理数x、y、z,满足x2-y2=y2-z2=A,证明:存在一个三边长都是有理数的直角三角形,它的面积等于A.
解:(1)设a,b,c是直角三角形的三边长,a,b,c都是有理数,且a
2+b
2=c
2,

ab=A,
若a=b,则2a
2=c
2,

=

,这与a,c都是有理数的假定矛盾,故a≠b.
不妨设a<b,取x=

,y=

,z=
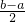
,则x,y,z都是有理数,
且x
2-y
2=

=

ab=A,y
2-z
2=
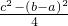
=

ab=A.
(2)设三个有理数x,y,z满足x
2-y
2=y
2-z
2=A,则x>y>z,取a=x-z,b=x+z,c=2y,则a,b,c都是有理数,
且a
2+b
2=2(x
2+z
2)=4y
2=c
2,

ab=

(x
2-z
2)=

[(x
2-y
2)+(y
2-z
2)]=A.
即存在一个三边长a,b,c都是有理数的直角三角形,它的面积等于A.
分析:(1)设a,b,c是直角三角形的三边长,a,b,c都是有理数,且a
2+b
2=c
2,

ab=A,由若a=b,求得

=

,可知a≠b;所以设a<b,x=

,y=

,z=
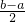
即可证得结论;
(2)设三个有理数x,y,z满足x
2-y
2=y
2-z
2=A,则x>y>z,取a=x-z,b=x+z,c=2y,代入检验即可证得结论.
点评:此题考查了有理数知识与完全平方式的应用.题目难度较大,注意构造符合要求的有理数是解题的关键.

 ab=A,
ab=A, =
= ,这与a,c都是有理数的假定矛盾,故a≠b.
,这与a,c都是有理数的假定矛盾,故a≠b. ,y=
,y= ,z=
,z=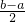 ,则x,y,z都是有理数,
,则x,y,z都是有理数, =
= ab=A,y2-z2=
ab=A,y2-z2=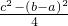 =
= ab=A.
ab=A. ab=
ab= (x2-z2)=
(x2-z2)= [(x2-y2)+(y2-z2)]=A.
[(x2-y2)+(y2-z2)]=A. ab=A,由若a=b,求得
ab=A,由若a=b,求得 =
= ,可知a≠b;所以设a<b,x=
,可知a≠b;所以设a<b,x= ,y=
,y= ,z=
,z=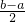 即可证得结论;
即可证得结论;

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案