
 ,tanβ=
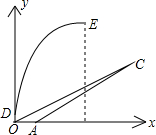
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中 E点).
E点). ,
, (x-12)2+20=-
(x-12)2+20=- x2+3x+2;
x2+3x+2; (2)设C(x1,y1),作CF⊥x轴,垂足为F,
(2)设C(x1,y1),作CF⊥x轴,垂足为F,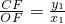 =
= ,
,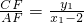 =
= ,
, x2+3x+2适合,
x2+3x+2适合,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| 5 |
| 2 |
| 3 |
 E点).
E点).查看答案和解析>>
科目:初中数学 来源:2005-2006学年广东省深圳市莲花中学九年级(上)期末数学试卷(解析版) 题型:解答题
 ,tanβ=
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
查看答案和解析>>
科目:初中数学 来源:2009-2010学年河南省周口市九年级(上)期末数学试卷(解析版) 题型:解答题
 ,tanβ=
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》常考题集(20):20.5 二次函数的一些应用(解析版) 题型:解答题
 ,tanβ=
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com