
 如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
如图,有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°. | 参考数据 | α=5° | α=12° | |
| sinα | 0.09 | 0.21 | |
| cosα | 0.10 | 0.98 | |
| tanα | 0.09 | 0.21 |
分析 (1)根据三角函数的定义直接求解即可.
(2)在△ACD中先求出AD长,再根据AB=AD-BD,即可得出答案.
解答 解:(1)在Rt△BCD中,
CD=BCsin12°≈10×0.21=2.1(米).
答:坡高CD的长是2.1米,
(2)在Rt△BCD中,
BD=BCcos12°≈10×0.98=9.8(米);
在Rt△ACD中,AD=$\frac{CD}{tan5°}$=$\frac{2.1}{0.09}$≈23.33(米),
AB=AD-BD≈23.33-9.8=13.53≈13.5(米),
答:斜坡新起点与原起点的距离为13.5米.
点评 此题考查了解直角三角形的应用-坡度坡角问题,这两个直角三角形有公共的直角边,先求出公共边是解决此类题目的基本出发点.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
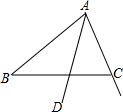 如图,在△ABC中,AB>AC,AD平分∠BAC
如图,在△ABC中,AB>AC,AD平分∠BAC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )
如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com