
在一次数学活动中,黑板上画着如图所示的图形,活动前刘老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
①AB=DC; ②∠ABE=∠DCE; ③AE=DE; ④∠A=∠D
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:
(1)请你写出在抽取的两张纸片上的等式为条件不能判断△BCE是等腰三角形的所有情形:
;(用序号表示)
(2)当抽得①和②时,用①,②作为条件能判定△BCE是等腰三角形吗?说说你的理由;
(1)若使△BEC为等腰三角形,即求解BE=CE即可.
若抽取的两张为①②,则可得出△ABE≌△DCE,∴BE=EC;
若是①③,AE=DE,AB=CD,并不能得出△ABE≌△DCE,∴这种情况不成立;
若是①④,则可得出△ABE≌△DCE,∴BE=EC;
若是②③,同样可得△ABE≌△DCE,∴BE=EC;
若是②④,三个角相等,但边长并不一定相等,则不成立,
若是③④,同样可得BE=EC.
故答案为:①③;②④.
(2)用①,②作为条件能判定△BCE是等腰三角形.
∵AB=DC,∠ABE=∠DCE,
又∵∠AEB=∠DEC
∴△ABE≌△DCE(AAS),
∴BE=EC,即△BCE是等腰三角形.
解析


科目:初中数学 来源: 题型:
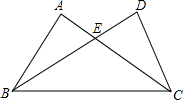 以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的概率.
以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的概率.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
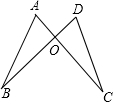
 8、在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:①AB=DC;②∠ABE=∠DCE;③AE=DE;④∠A=∠D;小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张,则以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的情况有
8、在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:①AB=DC;②∠ABE=∠DCE;③AE=DE;④∠A=∠D;小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张,则以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的情况有查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学活动中,黑板上画着如图所示的图形,活动前刘老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
在一次数学活动中,黑板上画着如图所示的图形,活动前刘老师在准备的四张纸片上分别写有如下四个等式中的一个等式:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com