
【题目】如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD,CE相交于F.
求证:AF平分∠BAC.

【答案】证明见解析
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分11分)学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
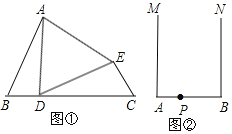
(1)如图①,∠B=∠C,BD=CE,AB=DC.
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
(2)如图②,射线AM与BN,AM⊥AB,BN⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点D满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种零件的内径尺寸在图纸上是50±0.05(单位:mm),表示这种零件的内径标准尺寸是多少?加工要求最大不超过标准尺寸多少毫米?符合要求的零件内径最小是多少毫米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?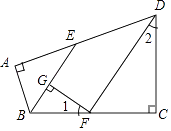
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
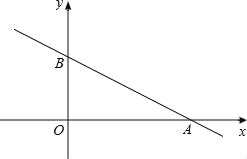
【题目】如图,在以点O为原点的直角坐标系中,一次函数y=﹣![]() x+1的图象与x轴交于A,与y轴交于点B,求:
x+1的图象与x轴交于A,与y轴交于点B,求:
(1)△AOB面积= ;
(2)△AOB内切圆半径= ;
(3)点C在第二象限内且为直线AB上一点,OC=![]() AB,反比例函数
AB,反比例函数![]() 的图象经过点C,求k的值.
的图象经过点C,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com