
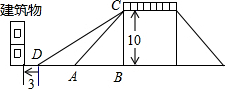
 (2013•黄埔区一模)为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.
(2013•黄埔区一模)为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.
| BC |
| sin∠CDB |
| 10 |
| sin28° |
| CB |
| DB |
| 10 |
| 17 |


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com