Question

如图，直线AC∥BD，连结AB，直线AC、BD把之间的平面分成①、②两个部分，规定线上各点不属于任何部分．当动点P落在某个部分时，连结PA、PB构成∠PAC、∠APB、∠PBD三个角．

（1）当动点P落在第①部分时，试说明：∠APB＝∠PAC＋∠PBD；（提示：过点P作直线与AC平行）

（2）当动点P落在第②部分时，请画出相应的图形．试探究∠APB、∠PAC、∠PBD之间的数量关系，并说明理由．

 

Answer 1

【答案】

（1）作PQ∥AC，则 PQ∥AC∥BD，根据平行线的性质可得∠APQ﹦∠CAP，∠BPQ﹦∠DPB，即可得到∠APB﹦∠APQ+∠BPQ﹦∠PAC+∠PBD；（2）∠APB+∠APC+∠PBD=360°

【解析】

试题分析：（1）作PQ∥AC，则 PQ∥AC∥BD，根据平行线的性质可得∠APQ﹦∠CAP，∠BPQ﹦∠DPB，即可得到∠APB﹦∠APQ+∠BPQ﹦∠PAC+∠PBD；

（2）根据平行线的性质可得∠APQ+∠PAC=180°，∠QPB+∠PBD=180°，即可得到结果.

（1）作PQ∥AC，则 PQ∥AC∥BD

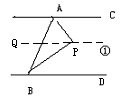
∴∠APQ﹦∠CAP，∠BPQ﹦∠DPB

∴∠APB﹦∠APQ+∠BPQ﹦∠PAC+∠PBD

（2）∠APB+∠APC+∠PBD=360°

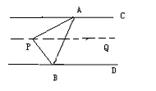
∵PQ∥AC∥BD 

∴∠APQ+∠PAC=180°，∠QPB+∠PBD=180°

∴∠APB+∠APC+∠PBD=360°.

考点：平行线的性质

点评：解题的关键是读懂题意及图形，正确作出辅助线，同时熟练掌握两直线平行，同位角相等，两直线平行，内错角相等，两直线平行，同旁内角互补.