
 的图象向上平移2个单位,得到一个新函数,平移前后的两个函数图象分
的图象向上平移2个单位,得到一个新函数,平移前后的两个函数图象分 别与y轴交于O、A两点,与直线
别与y轴交于O、A两点,与直线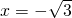 分别交于C、B两点.
分别交于C、B两点. 的图象的一部分,求满足条件的实数b的取值范围.
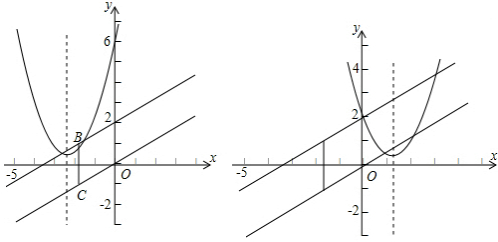
的图象的一部分,求满足条件的实数b的取值范围.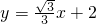 .
.
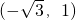 .
.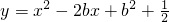 ,
,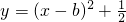
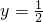 上移动
上移动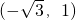 ,
,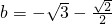 ,
,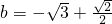 (不合题意,舍去)
(不合题意,舍去)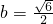 ,
,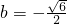 (不合题意,舍去)
(不合题意,舍去) .
. 的图象向上平移2个单位得出一个新函数为
的图象向上平移2个单位得出一个新函数为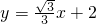 .
. 上移动.分别把点A、B代入二次函数求出b的取值范围.
上移动.分别把点A、B代入二次函数求出b的取值范围.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知:将函数
已知:将函数 的图象向上平移2个单位,得到一个新的函数图象.
的图象向上平移2个单位,得到一个新的函数图象.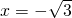 交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由;
交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由;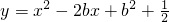 的图象一部分,求满足条件的实数b的取值范围.
的图象一部分,求满足条件的实数b的取值范围.查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省扬州市宜陵中学八年级上学期期末考试数学卷(带解析) 题型:填空题
将函数 的图象向上平移2个单位,所得函数图象的解析式为___________.
的图象向上平移2个单位,所得函数图象的解析式为___________.
查看答案和解析>>
科目:初中数学 来源:2011年江苏省盐城市中考数学考前测试卷(解析版) 题型:解答题
 的图象向上平移2个单位,得到一个新的函数图象.
的图象向上平移2个单位,得到一个新的函数图象. 交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由;
交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由; 的图象一部分,求满足条件的实数b的取值范围.
的图象一部分,求满足条件的实数b的取值范围.
查看答案和解析>>
科目:初中数学 来源:2010年北京市宣武区中考数学一模试卷(解析版) 题型:解答题
 的图象向上平移2个单位,得到一个新的函数图象.
的图象向上平移2个单位,得到一个新的函数图象. 交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由;
交于C,B两点.试判断以A,B,C,O四点为顶点四边形形状,并说明理由; 的图象一部分,求满足条件的实数b的取值范围.
的图象一部分,求满足条件的实数b的取值范围.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省扬州市八年级上学期期末考试数学卷(解析版) 题型:填空题
将函数 的图象向上平移2个单位,所得函数图象的解析式为___________.
的图象向上平移2个单位,所得函数图象的解析式为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com