

分析 (1)令y=0可求得点B的坐标为(3,0),令x=0,可求得点C的坐标为(0,4),由勾股定理可求得BC=5,然后由点A和点B的坐标可知AB=5,故此可证明△ABC为等腰三角形;
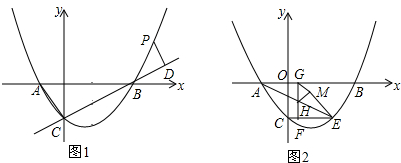
(2)①如图①当M在AO上时,过点N作NH⊥AB,垂足为H.由题意可求得$NH=\frac{4}{5}t$,MO=2-t,由三角形的面积公式可知S=$\frac{1}{2}$•OM•NH,从而可求得s与t的函数关系式;如图②所示:当M在OB上时,过点N作NH⊥AB,垂足为H.由题意可求得$NH=\frac{4}{5}t$,MO=t-2,由三角形的面积公式可知S=$\frac{1}{2}$•OM•NH,从而可求得s与t的函数关系式;将S=$\frac{21}{10}$代入函数解析式,的关于t的一元二次方程,从而可求得t的值;②当0<t≤2时,∠MON>90°的可能,所以△ONM为钝角三角形;当2<t<5时,当∠OMN=90°时,如图③所示:由$\frac{BM}{NB}=\frac{OB}{BC}$,列出关于t的方程求解即可;当t=5时.如图④,N与C重合,可得∠OMN=90°.
解答 解:(1)△ABC是等腰三角形.
理由:∵令y=0得:-$\frac{4}{3}x+4$=0,解得:x=3,
∴B(3,0).
∵当x=0时,y=4,
∴C(0,4).
在Rt△BOC中,OB=3,OC=4,由勾股定理可知:BC=$\sqrt{O{A}^{2}+O{B}^{2}}$=5.
∵点A的坐标是(-2,0),点B的坐标为(3,0),
∴BA=5.
∴BC=BA,
∴△ABC是等腰三角形.
(2)①如图①当M在AO上时,过点N作NH⊥AB,垂足为H.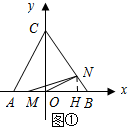
∵在Rt△BNH中,BN=t,$sinB=\frac{4}{5}$,
∴$NH=\frac{4}{5}t$.
∵OM=OA-AM,
∴MO=2-t.
∴S=$\frac{1}{2}$•OM•NH=$\frac{1}{2}$(2-t)×$\frac{4}{5}$t=-$\frac{2}{5}$t2+$\frac{4}{5}t$(0<t≤2).
如图②所示:当M在OB上时,过点N作NH⊥AB,垂足为H.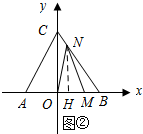
∵OM=AM-AO,
∴OM=t-2.
∴S=$\frac{1}{2}$•OM•NH=$\frac{1}{2}$(t-2)×$\frac{4}{5}$t=$\frac{2}{5}$t2-$\frac{4}{5}t$.(2<t≤5).
综上所述,S与t的函数关系式为S=$\left\{\begin{array}{l}{-\frac{2}{5}{t}^{2}+\frac{4}{5}t(0<t≤2)}\\{\frac{2}{5}{t}^{2}-\frac{4}{5}t(2<t≤5)}\end{array}\right.$.
把S=$\frac{21}{10}$代入S=$-\frac{2}{5}$t2+$\frac{4}{5}$t,得$-\frac{2}{5}$t2+$\frac{4}{5}$t=$\frac{21}{10}$,该方程无解,t值不存在.
把S=$\frac{21}{10}$代入S=$\frac{2}{5}$t2-$\frac{4}{5}$t,得$\frac{2}{5}$t2-$\frac{4}{5}$t=$\frac{21}{10}$,解得,t1=3.5,t2=-1.5(舍去负值).
因此,当t=3.5时,S=$\frac{21}{10}$.
②当0<t≤2时,∠MON>90°的可能,所以△ONM为钝角三角形.
当2<t<5时,当∠OMN=90°时,如图③所示: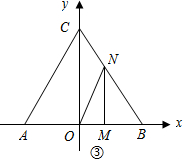
在Rt△BNM中,BN=t,BM=5-t,$cosB=\frac{3}{5}$,
∵MN∥OC,
∴$\frac{BM}{NB}=\frac{OB}{BC}$,即$\frac{5-t}{t}=\frac{3}{5}$.解得$t=\frac{25}{8}$.
当t=5时.如图④,N与C重合,可得∠OMN=90°.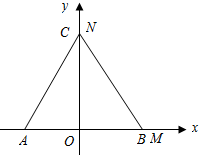
所以,当$t=\frac{25}{8}$或者t=5时,△MON为直角三角形.
综上所述t=5或t=$\frac{25}{8}$时,△MON为直角三角形.
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了坐标轴上点的坐标特点、三角形的面积公式、锐角三角形函数的定义,相似三角形的性质和判定、勾股定理的应用,根据题意画出符合题意得图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
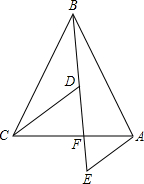 如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com