
分析 (1)设购买每辆A型公交车需要x万元,购买每辆B型公交车需要y万元,根据“若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买a辆A型公交车,则购买(10-a)辆B型公交车,根据总费用W不超过1200万元结合年均载客量总和不少于680万人次,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,由此即可得出各购买方程,再根据A型车费用低,即可得知选择第三种方案费用最低,根据总价=单价×数量列式计算,即可求出最少总费用.
解答 解:(1)设购买每辆A型公交车需要x万元,购买每辆B型公交车需要y万元,
根据题意得:$\left\{\begin{array}{l}x+2y=400\\ 2x+3y=650\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=100\\ y=150\end{array}\right.$.
答:购买A型和B型公交车每辆各需100万元、150万元.
(2)设购买a辆A型公交车,则购买(10-a)辆B型公交车,
根据题意得:$\left\{\begin{array}{l}{100a+150(10-a)≤1200}\\{60a+100(10-a)≥680}\end{array}\right.$,
解得:6≤a≤8,
∴有三种购车方案:①购买A型公交车6辆,B型公交车4辆;
②购买A型公交车7辆,B型公交车3辆;
③购买A型公交车8辆,B型公交车2辆.
∵A型公交车每辆的价格比B型公交车每辆价格便宜,即100万元<150万元,
∴购买A型公交车的数量最多,总费用最少,
∴选择第三种购车方案费用最少,
∴W=8×100+2×150=1100(万元).
答:该公司有3种购车方案,第3种购车方案的总费用最少,最少总费为1100万元.
点评 本题考查了一元一次不等式组的应用以及二元一次方程组的应用,解题的关键是:(1)找出等量关系,列出关于x、y的二元一次方程组:(2)根据各限定条件,列出关于a的一元一次不等式组.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
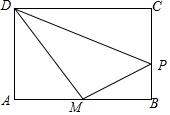 如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( )
如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.
画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面直角坐标系中,直线y=$\frac{4}{3}$x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.动点P为CD上一点,PH⊥OA,垂足为H,点Q是点B关于点A的对称点,当BP+PH+HQ值最小时,点P的坐标为(-4,4).
如图,平面直角坐标系中,直线y=$\frac{4}{3}$x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.动点P为CD上一点,PH⊥OA,垂足为H,点Q是点B关于点A的对称点,当BP+PH+HQ值最小时,点P的坐标为(-4,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
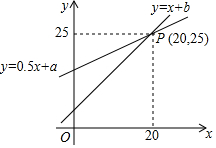 如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )| A. | x>25 | B. | x>20 | C. | x<25 | D. | x<20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com