
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=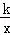 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
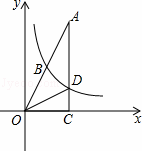
科目:初中数学 来源: 题型:
三个小球上分别标有-2,0,1三个数,这三个球除了标的数不同外,其余均相同.将
小球放入一个不透明的布袋中搅匀.
(1)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸
出一个小球,再记下小球上所标之数.求两次记下之数的和大于0的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,将小球上所标之数再记下,…,这样一共摸了13次.若记下的13个数之和等于-4,平方和等于14,求:这13次摸球中,摸到球上所标之数是0的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
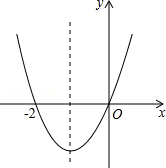
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:
①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
A.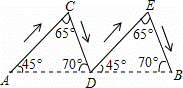 B.
B.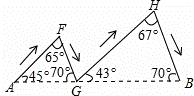
C.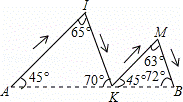 D.
D.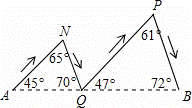
查看答案和解析>>
科目:初中数学 来源: 题型:
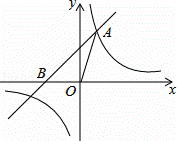
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=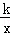 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北,据统计, 2014年“快的打车”账户流水总
2014年“快的打车”账户流水总 金额达到47.3亿元,47.3亿用科学计数法表示为( )
金额达到47.3亿元,47.3亿用科学计数法表示为( )
A B C D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com