Question

4．如图，等边△ABC中，D、E分别在边AB、AC上，且AD=CE，连接并延长BE、CD，交点为P，并使BG=CF，直线GA、BF交于点Q，过点A作AH⊥BF交BF延长线于H．
（1）如图（1），求证：∠GAH=∠BPC+30°；
（2）如图（2），在（1）的条件下，若D为AB中点，试探究线段QD与线段QC的数量关系，并加以证明．

Answer 1

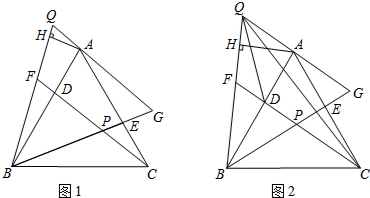
分析 （1）如图1，易证△BDC≌△AEB，则有∠DCB=∠EBA，由此可推出∠FPG=120°，易证△BFC≌△AGB，则有∠BFC=∠AGB，由此可得到∠AGB+∠HFP=180°，在五边形AHFPG中，由五边形的内角和为540°可求出∠GAH=150°，即可证到∠GAH=∠BPC+30°；
（2）连接HD，如图2，易证$\frac{QH}{QA}$=$\frac{HD}{AC}$=$\frac{1}{2}$，∠QHD=∠QAC，则有△QHD∽△QAC，然后根据相似三角形的性质就可得到QD=$\frac{1}{2}$QC．

解答 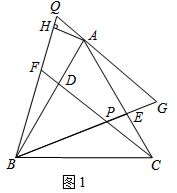（1）证明：如图1，
∵△ABC是等边三角形，
∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°．
∵AD=CE，
∴BD=AE．
在△BDC和△AEB中，
$\left\{\begin{array}{l}{BD=AE}\\{∠DBC=∠EAB}\\{BC=AB}\end{array}\right.$，
∴△BDC≌△AEB
∴∠DCB=∠EBA，
∴∠BPC=∠FPG=∠BDC+∠EBA=∠BDC+∠DCB
=180°-∠DBC=180°-60°=120°．
在△BFC和△AGB中，
$\left\{\begin{array}{l}{BC=AB}\\{∠BCF=∠ABG}\\{FC=BG}\end{array}\right.$，
∴△BFC≌△AGB，
∴∠BFC=∠AGB．
∵∠BFC+∠HFP=180°，
∴∠AGB+∠HFP=180°．
在五边形AHFPG中，
∵∠GAH+∠AHF+∠HFP+∠FPG+∠AGP=540°，
∠AGP+∠HFP=180°，∠AHF=90°，∠FPG=120°，
∴∠GAH=150°，
∴∠GAH=∠BPC+30°；

（2）QD=$\frac{1}{2}$QC．
证明：连接HD，如图2，
在Rt△AHB中，
∵点D为AB的中点，
∴HD=AD=$\frac{1}{2}$AB=$\frac{1}{2}$AC，
∴∠DHA=∠DAH，
∴∠QHD=90°+∠DHA．
∵∠QAC=∠QAH+∠DAH+∠BAC=90°+∠DAH，
∴∠QHD=∠QAC．
在Rt△AHQ中，
∵∠QAH=180°-∠GAH=30°，
∴QH=$\frac{1}{2}$QA．
∵$\frac{QH}{QA}$=$\frac{HD}{AC}$=$\frac{1}{2}$，∠QHD=∠QAC，
∴△QHD∽△QAC，
∴$\frac{QD}{QC}$=$\frac{QH}{QA}$=$\frac{1}{2}$，
∴QD=$\frac{1}{2}$QC．

点评 本题主要考查了相似三角形的判定与性质、全等三角形的判定与性质、等边三角形的性质、等腰三角形的性质、多边形的内角和定理、三角形外角的性质、30°角所对的直角边等于斜边的一半、直角三角形斜边上的中线等于斜边的一半等知识，有一定的综合性，运用相似三角形的性质是解决第（2）小题的关键．