
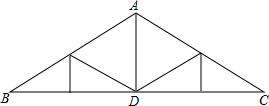
 如图,这是建筑物上的人字架,已知:AB=AC,AD⊥BC,则BD与CD相等吗?为什么?
如图,这是建筑物上的人字架,已知:AB=AC,AD⊥BC,则BD与CD相等吗?为什么?科目:初中数学 来源: 题型:
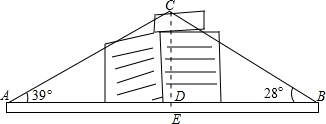 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
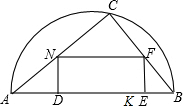 如图,在直径为AB的半圆内,画出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形建筑物DEFN,其中DE在AB上,设计方案是使AC=8,BC=6.
如图,在直径为AB的半圆内,画出一个三角形区域,使三角形的一边为AB,顶点C在半圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形建筑物DEFN,其中DE在AB上,设计方案是使AC=8,BC=6.查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(36):25.3 解直角三角形(解析版) 题型:解答题
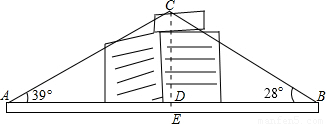 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com