
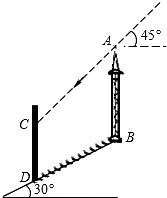
 如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号). 分析 过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,在Rt△BFD中,分别求出DF、BF的长度,在Rt△ACE中,求出AE、CE的长度;然后根据矩形BFCE的性质得到:CF=BE=CD-DF=1,然后通过解Rt△ACE求得AE=CE,结合图形来求得AB的长度.
解答 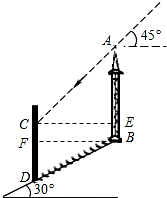 解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,
解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,
在Rt△BFD中,
∵∠DBF=30°,sin∠DBF=$\frac{DF}{BD}$=$\frac{1}{2}$,cos∠DBF=$\frac{BF}{BD}$=$\frac{\sqrt{3}}{2}$,
∵BD=4,
∴DF=2,BF=2$\sqrt{3}$,
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=2$\sqrt{3}$(米)
∵四边形BFCE为矩形,BF=CE=2$\sqrt{3}$.则CF=BE=CD-DF=1,
在Rt△ACE中,∠ACE=45°,
∴AE=CE=2$\sqrt{3}$米,
∴AB=2$\sqrt{3}$+1.
即:铁塔AB的高为(2$\sqrt{3}$+1)米.
点评 本题考查了解直角三角形的应用,解答本题的根据题目所给的坡角构造直角三角形,利用三角函数的知识求解.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且EG⊥CG于G,下列说法:
如图,在△ABC的角平分线CD,BE相交于F,∠A=90°,EG∥BC,且EG⊥CG于G,下列说法:| A. | 只有①③ | B. | 只有②④ | C. | 只有①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
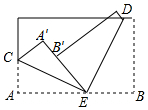 将一张长方形纸片按如图所示的方式折叠,EC,ED为折痕,折叠后点A′,B′,E在同一直线上,则∠CED的度数为( )
将一张长方形纸片按如图所示的方式折叠,EC,ED为折痕,折叠后点A′,B′,E在同一直线上,则∠CED的度数为( )| A. | 90° | B. | 75° | C. | 60° | D. | 95° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,AM⊥BC,AN⊥CD,M,N分别为垂足,求证:$\frac{AM}{AB}=\frac{MN}{AC}$.
如图,在平行四边形ABCD中,AM⊥BC,AN⊥CD,M,N分别为垂足,求证:$\frac{AM}{AB}=\frac{MN}{AC}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
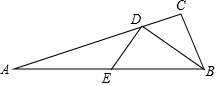 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE⊥BD交AB于D,若AD=$\sqrt{2}$AE,则cosA的值为$\frac{2\sqrt{2}}{3}$.
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE⊥BD交AB于D,若AD=$\sqrt{2}$AE,则cosA的值为$\frac{2\sqrt{2}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
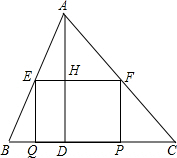 如图所示,在△ABC中,∠C=45°,BC=20,高AD=8.矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图所示,在△ABC中,∠C=45°,BC=20,高AD=8.矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com