

分析 (1)利用相似三角形的判断和性质,表示出BQ=t,QH=$\frac{4}{5}$t,PF=$\frac{5}{6}$t,相似三角形的面积比等于相似比的平方,S△CPF=$\frac{12}{25}$t2,从而y用三角形的面积的差表示出,即可;
(2)假设存在,建立方程,求出方程的解,全不符合题意,得到不存在;
(3)假设存在,建立方程,求出方程的解符合题意,即存在时间t,使PQ⊥PE;
(4)假设存在,由线段PQ的垂直平分线恰好经过点B,得到BQ=BP,建立方程,求出t,即可.
解答 解:如图1,作AG⊥BC于G,作QH⊥BC于H,
∴QH∥AG,
∴$\frac{BQ}{AB}$=$\frac{QH}{AG}$,
∵AG⊥BC,AB=AC=10,BC=12,
∴BG=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6,AG=8,
∵BQ=t,
∴$\frac{t}{10}$=$\frac{QH}{8}$,
∴QH=$\frac{4}{5}$t,
∵PE∥AB,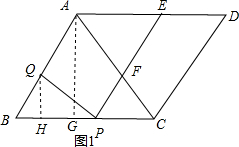
∴$\frac{PF}{AB}$=$\frac{PC}{BC}$,
∴$\frac{PF}{10}$=$\frac{t}{12}$,
∴PF=$\frac{5}{6}$t,
∵BC=12,AG=8,
∴S△ABC=$\frac{1}{2}$×BC×AG=48,
(1)∵BP=AE=BC-PC=12-t,QH=$\frac{4}{5}$t,
∴S△BPQ=$\frac{1}{2}$BP×QH=$\frac{1}{2}$×(12-t)×$\frac{4}{5}$t,
∴y=S四边形AQPE=S四边形ABPE-S△BPQ=(12-t)×8-$\frac{1}{2}$×(12-t)×$\frac{4}{5}$t=$\frac{2}{5}$t2-$\frac{64}{5}$t+96,(0<t<10)
(2)解:假设存在某一时刻t,使四边形AQPE的面积为平行四边形ABCD面积的一半,
由(1)由S四边形AQPE=$\frac{2}{5}$t2-$\frac{64}{5}$t+96,
∴$\frac{2}{5}$t2-$\frac{64}{5}$t+96=48,
∴t=16$+2\sqrt{34}$,(不合题意),t=16-2$\sqrt{34}$,
∴存在这样某一时刻t=$\frac{32-4\sqrt{34}}{2}$,使四边形AQPE的面积为平行四边形ABCD面积的一半;
(3)解:假设存在某一时刻t,使PQ⊥PE,
∵PE∥AB,
∴∠BQP=90°,
∴∠BQP=∠AGB,∠B=∠B,
∴△BQP∽△BGA,
∴$\frac{BQ}{BG}=\frac{BP}{AB}$,
∵BG=6,BQ=t,BP=12-t,AB=10,
∴$\frac{t}{6}$=$\frac{12-t}{10}$,
∴t=$\frac{9}{2}$,
∴存在t=$\frac{9}{2}$,使PQ⊥PE;
(4)假设存在某一时刻t,使线段PQ的垂直平分线恰好经过点B,
∴BQ=BP,
当0<t<10时,
∵BP=12-t,BQ=t,
∴12-t=t,
∴t=6,
∴存在t=6,使线段PQ的垂直平分线恰好经过点B,
当10≤t<12时,
∵BQ=20-t,BP=12-t,
∴20-t=12-t,明显等式不成立,
∴不存在某一时刻t,使线段PQ的垂直平分线恰好经过点B,
即:存在t=6,使线段PQ的垂直平分线恰好经过点B.
点评 本题主要考查了相似三角形的性质和判定,计算图形面积的方法,解本题的关键是建立y与t的函数关系式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为( )
如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为( )| A. | (0,-$\frac{9}{2}$) | B. | (0,-$\frac{9}{4}$) | C. | (0,-$\frac{7}{2}$) | D. | (0,-$\frac{7}{4}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
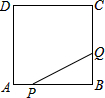 如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B-C-D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )
如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B-C-D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )| A. |  | B. | 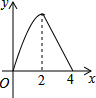 | C. | 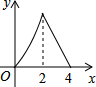 | D. | 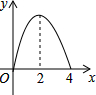 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com