
 为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)
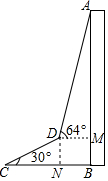
为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7) 分析 在Rt△CDN中求得BM=DN=$\frac{1}{2}$CD=10、CN=CDcos∠C=10$\sqrt{3}$,即可知DM=BN=50-10$\sqrt{3}$,根据AB=BM+AM=BM+DMtan∠ADN可得答案.
解答 解:在Rt△CDN中,∵CD=20米,∠C=30°,
∴BM=DN=$\frac{1}{2}$CD=10米,CN=CDcos∠C=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$米,
∵BC=50米,
∴DM=BN=BC-CN=50-10$\sqrt{3}$,
在Rt△ADN中,由tan∠ADN=$\frac{AM}{DM}$可得AM=DMtan∠ADN=(50-10$\sqrt{3}$)•tan64°,
则AB=AM+BM=(50-10$\sqrt{3}$)•tan64°+10≈79米,
答:楼AB的高度约为79米.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有实数根 | B. | 有实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
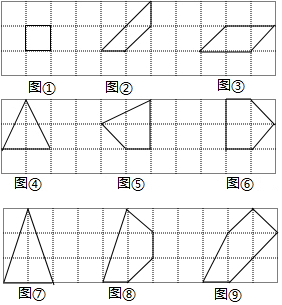
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ① | 0 | 4 | 1 |
| ② | 0 | 5 | 1.5 |
| ③ | 0 | 6 | 2 |
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ④ | 1 | 4 | 2 |
| ⑤ | 1 | 5 | 2.5 |
| ⑥ | 1 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com