
����Ŀ��ij�ľߵ꾭���ס������ֲ�ͬ�ıʼDZ�.��֪�����ֱʼDZ��Ľ���֮��Ϊ10Ԫ�����ֱʼDZ�ÿ������2Ԫ�����ֱʼDZ�ÿ������1Ԫ��������ͬѧ��4�����ֱʼDZ���3�����ֱʼDZ�������47Ԫ.
��1���ס������ֱʼDZ��Ľ��۷ֱ��Ƕ���Ԫ��
��2�����ľߵ깺�������ֱʼDZ���60�������Ѳ�����296Ԫ��������ֱʼDZ����ٱ�ʱ���ľߵ�������
��3��������ͳ�Ʒ���ƽ��ÿ����۳����ֱʼDZ�350�������ֱʼDZ�150��.������ֱʼDZ����ۼ�ÿ���1Ԫ����ÿ�콫���۳�50�����ֱʼDZ���������ֱʼDZ����ۼ�ÿ���1Ԫ����ÿ�����۳�40�����ֱʼDZ���Ϊʹÿ���ȡ��������࣬�������������ֱʼDZ��ļ۸����![]() Ԫ���ڲ������������ص������£���
Ԫ���ڲ������������ص������£���![]() ��Ϊ����Ԫʱ������ʹ���ľߵ�ÿ�����ۼס������ֱʼDZ���ȡ���������
��Ϊ����Ԫʱ������ʹ���ľߵ�ÿ�����ۼס������ֱʼDZ���ȡ���������
���𰸡���1�����ֱʼDZ��Ľ���Ϊ6Ԫ/�������ֱʼDZ��Ľ���Ϊ4Ԫ/����
��2��28
��3����x��Ϊ2Ԫʱ������ʹ���ľߵ�ÿ�����ۼס��ұʼDZ���ȡ����������������Ϊ1260Ԫ��
��������
��1������ֱʼDZ��Ľ���ΪmԪ/���������ֱʼDZ��Ľ���Ϊ��10-m��Ԫ/���������ܼ�=���ۡ����������ɵó�����m��һԪһ�η��̣���⼴��,
��2���蹺����ֱʼDZ�n�����������ֱʼDZ���60-n���������ݻ��Ѳ�����296Ԫ�����ɵó�����n��һԪһ�β���ʽ�飬��֮���ɵó�n��ȡֵ��Χ���ٽ��nΪ�����������ɽ���,
��3��������ֱʼDZ��ļ۸����xԪ��������ΪwԪ������������=����������������������ɵó�w����x�ĺ�����ϵʽ�������䷽����϶��κ��������ʼ��ɽ����ֵ���⣮
�⣺��1������ֱʼDZ��Ľ���ΪmԪ/���������ֱʼDZ��Ľ���Ϊ��10-m��Ԫ/����
��������ã�4��m+2��+3��10-m+1��=47��
��ã�m=6��
��10-m=4��
�𣺼��ֱʼDZ��Ľ���Ϊ6Ԫ/�������ֱʼDZ��Ľ���Ϊ4Ԫ/����
��2���蹺����ֱʼDZ�n�����������ֱʼDZ���60-n������
��������ã�6n+4(60-n)![]() 296,
296,
��ã� n��28,
������=2n+(60-n)=n+60,
��һ����ϵ������0,
��������n�����������,
��n��������
��n=28ʱ, ���ľߵ�������Ϊ88,
��3��������ֱʼDZ��ļ۸����xԪ��������ΪwԪ��
��������ã�w=��2+x����350-50x��+��1+x����150-40x��=-90��x-2��2+1260��
����w=-90��x-2��2+1260��a=-90��0��
�൱x=2ʱ��wȡ���ֵ�����ֵΪ1260,
�𣺵�x��Ϊ2Ԫʱ������ʹ���ľߵ�ÿ�����ۼס��ұʼDZ���ȡ����������������Ϊ,1260Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OAB�У���AOB=100�㣬OA=12��C��OB���е㣬CD��OB��![]() �ڵ�D����OCΪ�뾶��
�ڵ�D����OCΪ�뾶��![]() ��OA�ڵ�E����ͼ����Ӱ���ֵ�����ǣ�������
��OA�ڵ�E����ͼ����Ӱ���ֵ�����ǣ�������

A. 12��+18![]() B. 12��+36
B. 12��+36![]() C. 6��+18
C. 6��+18![]() D. 6��+36
D. 6��+36![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȷ�����ǡ�����ѧʷ��һ���������⣬����������̽���������Ѿ�ȷ�ţ�����Բ��ֱ���Dz�����������.��̽�������У����Ƿ��֣���������һЩ�����ͼ�Σ���һ����������ȷ�.��ͼ���ڡ�MAN�ı�����ȡһ��B������B��BC��AN�ڵ�C������BC�Ĵ���BF������AF��E��AF��һ�㣬��AB=BE=EFʱ���С�FAN=![]() ��MAN������֤��.
��MAN������֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC��90�㣬AB��8cm��AC��6cm������P�ӵ�C������CB������3cm/s���ٶ����B�˶���ͬʱ����Q�ӵ�B������BA������2cm/s���ٶ����A�˶�������APQ��ֱ��AB���۵á�AP��Q�����ı���APQP��Ϊ���Σ����˶�ʱ��Ϊ��������
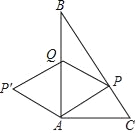
A. 1sB. ![]()
![]() sC.
sC. ![]() sD.
sD. ![]() s
s
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ھ���ABCD��,AB��BC=3��5,��E�ǶԽ���BD��һ����(�����B,D�غ�),�������ع���E��ֱ��MN�۵�,ʹ�õ�A,B�Ķ�Ӧ��G,F�ֱ���ֱ��AD��BC��,����DEFΪֱ��������ʱ,CN:BN��ֵΪ______.
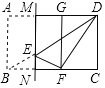
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶� AB �ij�Ϊ 4��C Ϊ AB ��һ�����㣬�ֱ��� AC��BC Ϊб���� AB ��ͬ������������ֱ�������� ACD �� BCE�� ���� DE�� �� DE ������Сֵ��( )
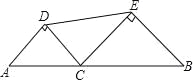
A. ![]() B. 2C.
B. 2C. ![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������κ���y=ax2+bx+c��ͼ����x�������������㣬��ôһԪ���η���ax2+bx+c=0����������ȵ�ʵ������������������仰�����⣬����������⣺��m��n��m��n���ǹ���x�ķ���1����x��a����x��b��=0����������a��b����a��b��m��n�Ĵ�С��ϵ�ǣ� ����
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����˹���������һ����ɽ����ɽ������һ����Ľ�����CD����Ϊ10�ף���ѧС��Ϊ�˲�����ɽ�ĸ߶�DE���ڹ�����һˮƽ���棬��A����ý������D����ɽ����������Ϊ35�㣬��ˮƽ����ǰ��20����B�㣬��ý����ﶥ��C�������Ϊ45�㣬���ɽ�ĸ߶�DE���������ȷ��1�ף��ο����ݣ�sin35���![]() ��cos35���
��cos35���![]() ��tan35���
��tan35���![]() ��
��
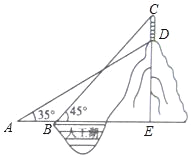
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
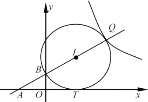
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=kx+1(k>0)��x�ᡢy��ֱ��ཻ�ڵ�A��B��tan��ABO=![]() ��
��
��1����k��ֵ��
��2����ֱ��l��y=kx+1��˫����y=![]() (
(![]() )��һ������Q��һ�����ڣ���BQΪֱ���ġ�I��x�������ڵ�T����m��ֵ��
)��һ������Q��һ�����ڣ���BQΪֱ���ġ�I��x�������ڵ�T����m��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com