
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= ![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C. 
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b﹣ ![]() <0的解集.(直接写出答案)
<0的解集.(直接写出答案)
【答案】
(1)解:∵B(1,4)在反比例函数y= ![]() 上,
上,
∴m=4,
又∵A(n,﹣2)在反比例函数y= ![]() 的图象上,
的图象上,
∴n=﹣2,
又∵A(﹣2,﹣2),B(1,4)是一次函数y=kx+b的上的点,联立方程组解得,
k=2,b=2,
∴ ![]() ,y=2x+2;
,y=2x+2;
(2)解:过点A作AD⊥CD,

∵一次函数y=kx+b的图象和反比例函数y= ![]() 的图象的两个交点为A,B,联立方程组解得,
的图象的两个交点为A,B,联立方程组解得,
A(﹣2,﹣2),B(1,4),C(0,2),
∴AD=2,CO=2,
∴△AOC的面积为:S= ![]() ADCO=
ADCO= ![]() ×2×2=2;
×2×2=2;
(3)解:由图象知:当0<x<1和﹣2<x<0时函数y= ![]() 的图象在一次函数y=kx+b图象的上方,
的图象在一次函数y=kx+b图象的上方,
∴不等式kx+b﹣ ![]() <0的解集为:0<x<1或x<﹣2.
<0的解集为:0<x<1或x<﹣2.
【解析】(1)由B点在反比例函数y= ![]() 上,可求出m,再由A点在函数图象上,由待定系数法求出函数解析式;(2)由上问求出的函数解析式联立方程求出A,B,C三点的坐标,从而求出△AOC的面积;(3)由图象观察函数y=
上,可求出m,再由A点在函数图象上,由待定系数法求出函数解析式;(2)由上问求出的函数解析式联立方程求出A,B,C三点的坐标,从而求出△AOC的面积;(3)由图象观察函数y= ![]() 的图象在一次函数y=kx+b图象的上方,对应的x的范围.
的图象在一次函数y=kx+b图象的上方,对应的x的范围.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,3)、B(3,3)、C(4,2). 
(1)请在图中作出经过点A、B、C三点的⊙M,并写出圆心M的坐标;
(2)若D(1,4),则直线BD与⊙M .
A.相切
B.相交.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,点D在线段BC的延长线上移动,若∠BAC=40![]() ,求∠DCE的度数.
,求∠DCE的度数.
(2)设∠BAC=m,∠DCE=n.
①如图,当点D在线段BC的延长线上移动时,m与n之间有什么数量关系?请说明理由.
②当点D在直线BC上(不与B、C重合)移动时,m与n之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过点D分别向AB、AC引垂线,垂足分别为点E、F.
(1)如图①,当点D在BC的什么位置时,DE=DF?并证明;
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?请写出所有的全等三角形(不必证明);
(3)如图②,过点C作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 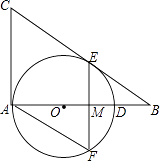
(1)若AC=5,BC=13,求⊙O的半径;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
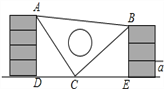
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com