
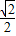 a,再利用正八边形周围四个三角形的特殊性得出阴影部分面积即可.
a,再利用正八边形周围四个三角形的特殊性得出阴影部分面积即可.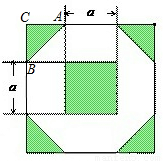 解:∵某小区将原来正方形地砖更换为如图所示的正八边形植草砖,设正八边形与其内部小正方形的边长都为a,
解:∵某小区将原来正方形地砖更换为如图所示的正八边形植草砖,设正八边形与其内部小正方形的边长都为a,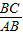 =
=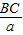 =
=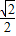 ,
,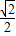 a,
a, ×
×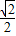 a×
a×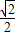 a=
a=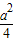 ,
, ×4=a2.
×4=a2.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
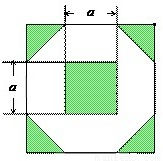
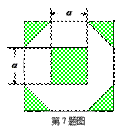
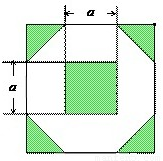
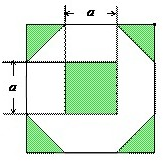 (2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
(2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )查看答案和解析>>
科目:初中数学 来源: 题型:
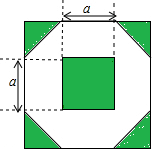 为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为![]() ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A.2![]() B. 3
B. 3![]() C. 4
C. 4![]() D.5
D.5![]()
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(安徽卷)数学(解析版) 题型:选择题
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为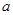 ,则阴影部分的面积为【 】
,则阴影部分的面积为【 】
A.2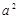 B. 3
B. 3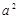 C. 4
C. 4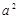 D.5
D.5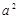
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com