分析:(1)想要建立起以x为自变量的函数y的解析式,则必须要找出中间的等量关系,利用这个等量关系,把y用x表示出来.
(2)根据x的取值范围,利用二次函数最值的求法即可解出此问.
解答: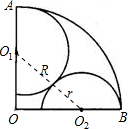
解:(1)设两圆半径分别为R、r,
y=π(R2+r2),
x=r+R,
通过变形把R
2和r
2用“x=R+r”的代数式表示,作基本辅助线,如图,半径分别为r、R的圆1、圆2外切于C,连接O
1O
2.
y=
π (R2+ r2)=
π[(R+r)2-2Rr],
且有(R+r)
2=(1-R)
2+(1-r)
2,化简得:r+R+Rr=1,
所以:y=
π{(R+r)2-2[1-(R+r)] }=(x2+2x-2),
所以建立的以x为自变量的函数y的解析式为:y=
π{(R+r)2-2[1-(R+r)] }=(x2+2x-2),
(2)∵(
-
)
2≥0,
∴R+r≥
2,
∴
≥Rr,Rr=1-(R+r),
∴(R+r)
2+4(R+r)-4≥0,
又∵R+r≥0,
∴R+r≥2
-2,即x≥2
-2,
故函数:y=
π{(R+r)2-2[1-(R+r)] }=(x2+2x-2),
当x=2
-2时,有
ymin=(3-2)π,
答:函数y的最小值为
ymin=(3-2)π.
点评:本题看似考查几何,实际考查的还是二次函数问题,以及二次函数的最值求法.

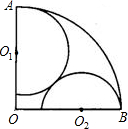 在OB上,并与弧AB内切于点B,半圆O1与半圆O2相切,设两半圆的半径之和为x,面积之和为y.
在OB上,并与弧AB内切于点B,半圆O1与半圆O2相切,设两半圆的半径之和为x,面积之和为y. 解:(1)设两圆半径分别为R、r,
解:(1)设两圆半径分别为R、r,

 在OB上,并与弧AB内切于点B,半圆O1与半圆O2相切,设两半圆的半径之和为x,面积之和为y.
在OB上,并与弧AB内切于点B,半圆O1与半圆O2相切,设两半圆的半径之和为x,面积之和为y.
