解:(1)设反比例函数解析式为y=

(k≠0),
由一次函数与反比例函数都经过A(-2,-1),
故将x=-2,y=-1代入反比例解析式得:-1=
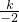
,
解得:k=2,
∴反比例函数解析式为y=

;
又B(n,2)在反比例函数图象上,
∴将x=n,y=2代入反比例函数解析式得:2=

,
解得:n=1,即B(1,2),
设一次函数解析式为y=px+q(p≠0),
将A和B的坐标代入得:
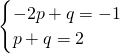
,
解得:
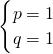
,
∴一次函数解析式为y=x+1;
(2)设一次函数与x轴交于C点,过A作AD⊥x轴于D点,过B作BE⊥x轴于E点,如图所示:
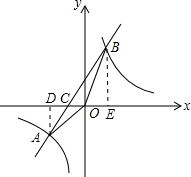
对应一次函数y=x+1,令y=0,解得:x=-1,故C(-1,0),即OC=1,
又A(-2,-1),B(1,2),
∴AD=1,BE=2,
则S
△OAB=S
△AOC+S
△BOC=

OC•AD+

OC•BE=

+1=

.
分析:(1)由一次函数与反比例函数图象交于A和B两点,故设出反比例函数解析式y=

(k≠0),将A的坐标代入求出k的值,确定出反比例解析式,将B的坐标代入反比例解析式中求出n的值,确定出B的坐标,设一次函数解析式为y=px+q(p≠0),将A与B的坐标代入一次函数解析式中,得到关于p与q的方程组,求出方程组的解得到p与q的值,确定出一次函数解析式;
(2)令(1)求出的一次函数解析式y=0,求出对应x的值,确定出C的坐标,得到OC的长,过A作AD⊥x轴于D点,过B作BE⊥x轴于E点,如图所示,可得出AD即为A纵坐标的绝对值,BE为B纵坐标的绝对值,三角形AOB的面积=三角形AOC的面积+三角形BOC的面积,求出即可.
点评:此题考查了一次函数与反比例函数图象的交点,待定系数法求函数解析式,坐标与图形性质,以及三角形面积的求法,利用了数形结合及转化的思想,灵活运用待定系数法是解本题的关键.

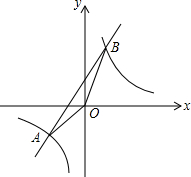 己知一次函数与反比例函数图象都经过A(-2,-1)、B(n,2)两点.
己知一次函数与反比例函数图象都经过A(-2,-1)、B(n,2)两点. (k≠0),
(k≠0),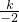 ,
, ;
; ,
,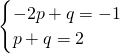 ,
,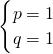 ,
,
 OC•AD+
OC•AD+ OC•BE=
OC•BE= +1=
+1= .
. (k≠0),将A的坐标代入求出k的值,确定出反比例解析式,将B的坐标代入反比例解析式中求出n的值,确定出B的坐标,设一次函数解析式为y=px+q(p≠0),将A与B的坐标代入一次函数解析式中,得到关于p与q的方程组,求出方程组的解得到p与q的值,确定出一次函数解析式;
(k≠0),将A的坐标代入求出k的值,确定出反比例解析式,将B的坐标代入反比例解析式中求出n的值,确定出B的坐标,设一次函数解析式为y=px+q(p≠0),将A与B的坐标代入一次函数解析式中,得到关于p与q的方程组,求出方程组的解得到p与q的值,确定出一次函数解析式;

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案 (任选一题,若两题都选按得分最少的题记分,本题最高10分)
(任选一题,若两题都选按得分最少的题记分,本题最高10分) 探索研究:
探索研究: (1)已知:如下图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)已知:如下图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).