
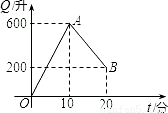
 解:(1)10分钟进水600升,每分钟进水600÷10=60升;20分钟时进水60×20=1200升,还剩水200升,出水1000升,后10分钟每分钟放水1000÷10=100升.
解:(1)10分钟进水600升,每分钟进水600÷10=60升;20分钟时进水60×20=1200升,还剩水200升,出水1000升,后10分钟每分钟放水1000÷10=100升.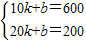 解得
解得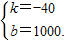


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
 (2012•甘井子区模拟)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为
(2012•甘井子区模拟)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•甘井子区模拟)学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为
(2012•甘井子区模拟)学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com