如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.
(1)若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形,求b的值;
(2)若△OAB是“抛物线三角形”,其中点B为顶点,抛物线三角形系数为[-2,2m,0],其中m>0;且四边形ABCD是以原点O为对称中心的矩形,求出过O、C、D三个点的抛物线的表达式.
解:(1)∵抛物线三角形系数为[-1,b,0],
∴抛物线解析式为y=-x
2+bx=-(x-

)
2+

,
∴顶点坐标为(

,

),
令y=0,则-x
2+bx=0,
解得x
1=0,x
2=b,
∴与x轴的交点为(0,0),(b,0),
∵“抛物线三角形”是等腰直角三角形,
∴

=

|b|,
∴b
2=2b或b
2=-2b,
∵b=0时,抛物线与x轴只有一个交点(0,0),
∴b=0不符合题意,
∴b=2或b=-2,
故b的值为2或-2;
(2)如图,∵四边形ABCD是矩形,
∴OA=OB,
由抛物线的对称性,OB=AB,
∴OA=OB=AB,
∴△AOB是等边三角形,

∵抛物线三角形系数为[-2,2m,0],
∴抛物线解析式为y=-2x
2+2mx=-2(x-

)
2+

,
∴顶点B的坐标为(

,

),
令y=0,则-2x
2+2mx=0,
解得x
1=0,x
2=m,
∴与x轴的交点为(0,0),(m,0),
∴AO=m,
∴

=

m,
解得m=

,
∴点A(

,0),B(

,

),
∵四边形ABCD是以原点O为对称中心的矩形,
∴点C(-

,0),D(-

,-

),
设过O、C、D三个点的抛物线为y=ax
2+bx(a≠0),
则
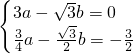
,
解得

,
所以,过O、C、D三个点的抛物线为y=2x
2+2

x.
分析:(1)把抛物线三角形系数代入抛物线,令y=0求出点A的坐标,再求出顶点坐标,然后根据等腰直角三角形的斜边上的高线等于斜边的一半列出方程求解即可得到b的值;
(2)根据矩形的对角线互相平分且相等可得OA=OB,再根据抛物线的对称性可得OB=AB,从而判定△AOB是等边三角形,然后抛物线三角形系数代入抛物线,令y=0求出点A的坐标,再求出顶点坐标,过然后根据等边三角形的高等于边长的

列出方程求出m的值,从而得到点A、B的坐标,再根据关于原点对称的点的横坐标与纵坐标都互为相反数求出C、D的坐标,再利用待定系数法求二次函数解析式解答即可.
点评:本题是二次函数综合题型,主要考查了等腰直角三角形的性质,等边三角形的判定与性质,矩形的对角线互相平分且相等的性质,待定系数法求二次函数解析式,读懂题目信息,理解“抛物线三角形”的定义是解题的关键.

 )2+
)2+ ,
, ,
, ),
), =
= |b|,
|b|,
 )2+
)2+ ,
, ,
, ),
), =
= m,
m, ,
, ,0),B(
,0),B( ,
, ),
), ,0),D(-
,0),D(- ,-
,- ),
),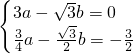 ,
, ,
, x.
x. 列出方程求出m的值,从而得到点A、B的坐标,再根据关于原点对称的点的横坐标与纵坐标都互为相反数求出C、D的坐标,再利用待定系数法求二次函数解析式解答即可.
列出方程求出m的值,从而得到点A、B的坐标,再根据关于原点对称的点的横坐标与纵坐标都互为相反数求出C、D的坐标,再利用待定系数法求二次函数解析式解答即可.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.