Question

两个等边三角形的面积比是3：4，则它们的边长比是    ，周长是    ．

Answer 1

【答案】分析：已知三角形面积比，根据等边三角形面积的计算可以求得三角形边长的比，即可求得周长比，即可解题．
解答：解：等边三角形ABC的面积为AB•BC•sinB，
等边三角形A′B′C′的面积为A′B′•B′C′•sinB′，
∵=，
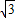
∴AB：A′B′=：2，
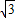
∴周长比为3AB：3A′B′=3：3×2=：2．
故答案为：2、：2．
点评：本题考查了等边三角形各边长相等的性质，考查了三角形面积计算公式，考查了相似三角形对应边比值相等的性质，本题中求AB：A′B′是解题的关键．