
 某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
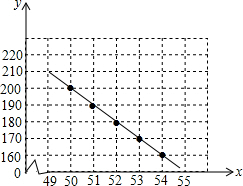
某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:| 销售单价x(元) | 50 | 51 | 52 | 53 | 54 |
| 每天的销售数量y(件) | 200 | 190 | 180 | 170 | 160 |
|
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
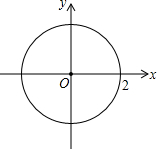 如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.
如图,⊙O的圆心是坐标原点,半径为2个单位,在坐标轴上找一点P,以P为圆心,1个单位长为半径作⊙P与⊙O相切,画出图形,并写出满足条件的所有点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com