
如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.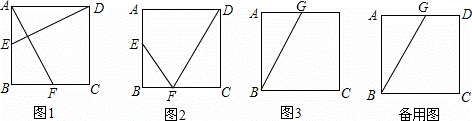
(1)点F在边BC上.
①如图1,连接DE,AF,若DE⊥AF,求t的值;
②如图2,连结EF,DF,当t为何值时,△EBF与△DCF相似?
(2)如图3,若点G是边AD的中点,BG,EF相交于点O,试探究:是否存在在某一时刻t,使得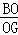 =?若存在,求出t的值;若不存在,请说明理由.
=?若存在,求出t的值;若不存在,请说明理由.
解:(1)①如图1
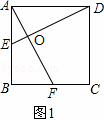
∵DE⊥AF,
∴∠AOE=90°,
∴∠BAF+∠AEO=90°,
∵∠ADE+∠AEO=90°,
∴∠BAE=∠ADE,
又∵四边形ABCD是正方形,
∴AE=AD,∠ABF=∠DAE=90°,
在△ABF和△DAE中,

 ∴△ABF≌△DAE(ASA)
∴△ABF≌△DAE(ASA)
∴AE=BF,
∴1+t=2t,
解得t=1.
②如图2
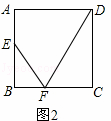
∵△EBF∽△DCF
∴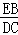 =
=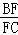 ,
,
∵BF=2t,AE=1+t,
∴FC=4﹣2t,BE=4﹣1﹣t=3﹣t,
∴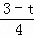 =
= ,
,
解得,t=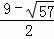 ,t=
,t=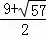 (舍去),
(舍去),
故t=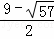 .
.
(2)①0<t≤2时如图3,以点B为原点BC为x轴,BA为y轴建立坐标系,
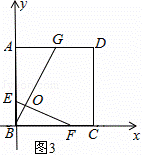
A的坐标(0,4),G的坐标(2,4),F点的坐标(2t,0),E的坐标(0,3﹣t)
EF所在的直线函数关系式是:y=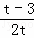 x+3﹣t,
x+3﹣t,
BG所在的直线函数关系式是:y=2x,
∵BG=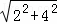 =2
=2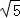
∵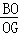 =,
=,
∴BO=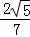 ,OG=
,OG=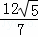 ,
,
设O的坐标为(a,b),
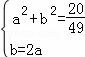
解得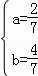
∴O的坐标为(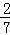 ,
,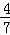 )
)
把O的坐标为(,)代入y=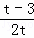 x+3﹣t,得
x+3﹣t,得
=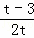 ×+3﹣t,
×+3﹣t,
解得,t=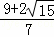 (舍去),t=
(舍去),t=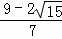 ,
,
②当3≥t>2时如图4,以点B为原点BC为x轴,BA为y轴建立坐标系,
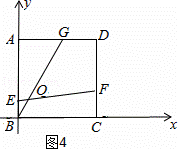

A的坐标(0,4),G的坐标(2,4),F点的坐标(4,2t﹣4),E的坐标(0,3﹣t)
EF所在的直线函数关系式是:y=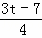 x+3﹣t,
x+3﹣t,
BG所在的直线函数关系式是:y=2x,
∵BG=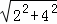 =2
=2
∵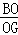 =,
=,
∴BO=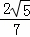 ,OG=
,OG= ,
,
设O的坐标为(a,b),
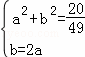
解得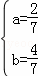
∴O的坐标为(,)
把O的坐标为(,)代入y=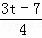 x+3﹣t,得
x+3﹣t,得
=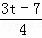 ×+3﹣t,
×+3﹣t,
解得:t= .
.
综上所述,存在t=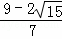 或t=
或t=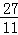 ,使得
,使得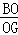 =
=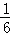 .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
在班级组织的“贵阳市创建国家环保模范城市”知识竞赛中,小悦所在小组8名同学的成绩分别为(单位:分)95,94,94,98,94,90,94,90,则这8名同学成绩的众数是( )
|
| A. | 98分 | B. | 95分 | C. | 94分 | D. | 90分 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的袋子中,装有大小、形状、质地等都相同的红色、黄色、白色小球各1个,从袋子中随机摸出一个小球,之后把小球放回袋子中并摇匀,再随机摸出一个小球,则两次摸出的小球颜色相同的概率是
查看答案和解析>>
科目:初中数学 来源: 题型:
某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目上,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 ”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
|
| A. | 0.25×10﹣5 | B. | 2.5×10﹣5 | C. | 2.5×10﹣6 | D. | 2.5×10﹣7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com