如图，已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点.
（1）求证MN⊥DE．
（2）连结DM，ME，猜想∠A与∠DME之间的关系，并写出推理过程．
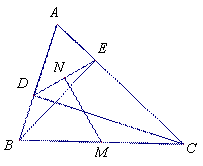
（3）若将锐角△ABC变为钝角△ABC，如图，上述（1）（2）中的结论是否都成立， 若结论成立，直接回答，不需证明；若结论不成立，说明理由．
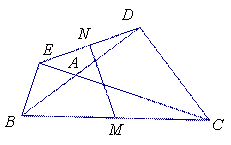
（1）连结DM，ME
可得DM=
BC，ME=BC，
DM=ME
又N为中点，∴MN⊥DE．……3分
（2）∠DME=180°－2∠A ……4分 推理过程略 ……6分
(3) 结论（1）成立，……7分
结论（2）不成立 ∠DME=2∠A－180°……9分
练习册系列答案
相关习题
科目：初中数学 来源： 题型： 如图，已知锐角△ABC的边BC的长为6，面积为12，PQ∥BC，点P在AB上，点Q在AC上，四边形RPQS为正方形（RS与A在PQ的异侧），其边长为x，正方形RPQS与△ABC的公共面积为y． （1）当正方形RPQS的边RS恰好落在BC上时，求边长x．   （2）当RS不落在BC上时，求y关于x的函数关系式以及自变量x的取值范围．（可以将图形画在备用的图形中）  （3）求y的最大值． 查看答案和解析>> 科目：初中数学 来源： 题型： （2011•裕华区二模）如图①，将两个等腰直角三角形叠放在一起，使上面三角板的一个锐角顶点与下面三角板的直角顶点重合，并将上面的三角板绕着这个顶点逆时针旋转，在旋转过程中，当下面三角板的斜边被分成三条线段时，我们来研究这三条线段之间的关系． （1）实验与操作： 如图②，如果上面三角板的一条直角边旋转到CM的位置时，它的斜边恰好旋转到CN的位置，请在网格中分别画出以AM、MN和NB为边长的正方形，观察这三个正方形的面积之间的关系； （2）猜想与探究： 如图③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB边上的点，∠MCN=45°，作DA⊥AB于点A，截取DA=NB，并连接DC、DM． 我们来证明线段CD与线段CN相等． ∵∠CAB=∠CBA=45°，又DA⊥AB于点A， ∴∠DAC=45°，∴∠DAC=∠CBA， 又∵DA=NB，BC=AC， ∴△CAD≌△CBN． ∴CD=CN．  请你继续解答： ①线段MD与线段MN相等吗？为什么？ ②线段AM、MN、NB有怎样的数量关系，为什么？ （3）拓广与运用： 如图④，已知线段AB上任意一点M（AM＜MB），是否总能在线段MB上找到一点N，使得分别以AM与BN为边长的正方形的面积的和等于以MN为边长的正方形的面积？若能，请在图④中画出点N的位置，并简要说明作法；若不能，请说明理由． 查看答案和解析>> 科目：初中数学 来源： 题型： 如图，已知锐角△ABC中，CD、BE分别是AB、AC边上的高，M、N分别是线段BC、DE的中点． （1）求证：MN⊥DE； （2）连结DM，ME，猜想∠A与∠DME之间的关系，并写出推理过程； （3）若将锐角△ABC变为钝角△ABC，如图，上述（1）（2）中的结论是否都成立？若结论成立，直接回答，不需证明；若结论不成立，说明理由．  查看答案和解析>> 科目：初中数学 来源： 题型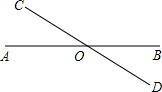：  如图，已知直线AB和CD相交于点O（∠AOC为锐角）（1）写出∠AOC和∠BOD的大小关系 ∠AOC=∠BOD ∠AOC=∠BOD ；判断的依据是对顶角相等 对顶角相等 ．（2）过点O作射线OE、OF，若∠COE=90°，OF平分∠AOE，画出图形并求∠AOF+∠COF的度数，说明你的理由． （3）在（2）的条件下，若∠AOD=120°，请计算∠COF的度数． 查看答案和解析>> 科目：初中数学 来源： 题型：解答题
|
如图，已知直线AB和CD相交于点O（∠AOC为锐角）