
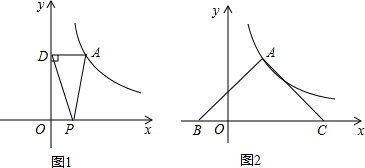
 已知点A(a,b)为双曲线
已知点A(a,b)为双曲线 (x>0)图象上一点.
(x>0)图象上一点.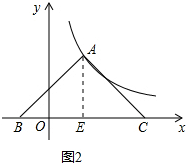 解:(1)由点A(a,b)在反比例函数
解:(1)由点A(a,b)在反比例函数 上可得:
上可得: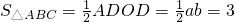 ,
,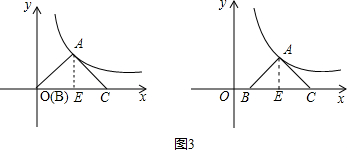 (3)由(2)可知:EC=AE=BE=b;且不管点A如何移动,总有:OC=OE+EC=a+b,且C总在x轴正半轴,
(3)由(2)可知:EC=AE=BE=b;且不管点A如何移动,总有:OC=OE+EC=a+b,且C总在x轴正半轴, 上可得到ab=6,AD=a,OD=b,进而根据三角形的面积公式求出△APD的面积;
上可得到ab=6,AD=a,OD=b,进而根据三角形的面积公式求出△APD的面积;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
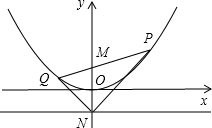
查看答案和解析>>
科目:初中数学 来源: 题型:
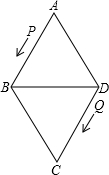 发沿线路DC?CB?BA做匀速运动.
发沿线路DC?CB?BA做匀速运动.查看答案和解析>>
科目:初中数学 来源: 题型:
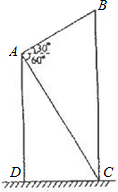 在一次数学课外活动中,一位同学在教学楼的点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为15cm.求旗杆的高度.
在一次数学课外活动中,一位同学在教学楼的点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为15cm.求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
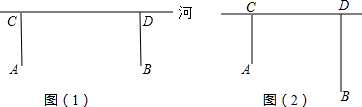
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com