
 如图,A,D是公园中人工湖边的两棵树,AB,BC,CD是公园内的甬路.小明同学想测出A,D两点间的距离.于是他进行了如下测量:B点在A点北偏东α方向,C点在B点北偏东β方向,C点在D点正东方向.你认为他还需要测出AB,BC,CD中哪些线段的长?并根据小明的测量和你的判断推导出AD的表达式.
如图,A,D是公园中人工湖边的两棵树,AB,BC,CD是公园内的甬路.小明同学想测出A,D两点间的距离.于是他进行了如下测量:B点在A点北偏东α方向,C点在B点北偏东β方向,C点在D点正东方向.你认为他还需要测出AB,BC,CD中哪些线段的长?并根据小明的测量和你的判断推导出AD的表达式.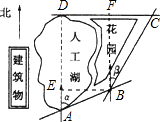 解:可以只测量AB,BC的长度.
解:可以只测量AB,BC的长度.

科目:初中数学 来源: 题型:
 在某城市的一个公园中,有一个较大的圆形区域可以利用,当地政府打算在这个地方修建一个菱形水池(如图,花坛中心A与圆心重合).修建方案呈送市长道利斯•匆明女士,市长很高兴.“菱形建筑红色瓷砖,真漂亮.请问这个水池每边多长?”建筑师福兰克•余春一时语塞.“让我想想,AB长5米,BC长4米,要求出BD的长度,恐怕要用一下勾股定理.”就在余春先生煞费苦心求解时,市长忽然嚷道:“很显然水池每边9米嘛!”余春先生恍然大悟,惭愧地说:“看来你的确是匆明(聪明),我真是余春(愚蠢)啊!”你知道问题怎么会这么简单吗?
在某城市的一个公园中,有一个较大的圆形区域可以利用,当地政府打算在这个地方修建一个菱形水池(如图,花坛中心A与圆心重合).修建方案呈送市长道利斯•匆明女士,市长很高兴.“菱形建筑红色瓷砖,真漂亮.请问这个水池每边多长?”建筑师福兰克•余春一时语塞.“让我想想,AB长5米,BC长4米,要求出BD的长度,恐怕要用一下勾股定理.”就在余春先生煞费苦心求解时,市长忽然嚷道:“很显然水池每边9米嘛!”余春先生恍然大悟,惭愧地说:“看来你的确是匆明(聪明),我真是余春(愚蠢)啊!”你知道问题怎么会这么简单吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com