
ĄŸÌâÄżĄżÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹĄŃO”İ럶ÎȘ1ŁŹPÊÇŚű±êÏ”ÄÚÈÎÒâÒ»”㣏”ăP”œĄŃO”ÄŸàÀëSP”ĶšÒćÈçÏÂŁșÈô”ăPÓëÔČĐÄOÖŰșÏŁŹÔòSPÎȘĄŃO”İ럶ł€Ł»Èô”ăPÓëÔČĐÄOČ»ÖŰșÏŁŹŚśÉäÏßOPœ»ĄŃOÓÚ”ăAŁŹÔòSPÎȘÏ߶ÎAP”Äł€¶ÈŁź
ÍŒ1ÎȘ”ăPÔÚĄŃOÍâ”ÄÇéĐÎÊŸÒâÍŒŁź
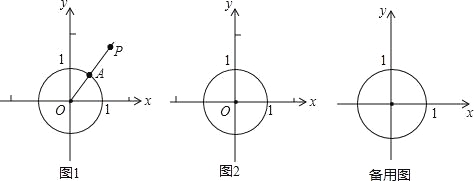
Łš1Ł©Èô”ăBŁš1ŁŹ0Ł©ŁŹCŁš1ŁŹ1Ł©ŁŹDŁš0ŁŹ![]() Ł©ŁŹÔòSB= Ł»SC= Ł»SD= Ł»
Ł©ŁŹÔòSB= Ł»SC= Ł»SD= Ł»
Łš2Ł©ÈôÖ±Ïßy=x+bÉÏŽæÔÚ”ăMŁŹÊč”ĂSM=2ŁŹÇób”ÄÈĄÖ”·¶Î§Ł»
Łš3Ł©ÒŃÖȘ”ăPŁŹQÔÚxÖáÉÏŁŹRÎȘÏ߶ÎPQÉÏÈÎÒâÒ»”㣟ÈôÏ߶ÎPQÉÏŽæÔÚÒ»”ăTŁŹÂúŚăTÔÚĄŃOÄÚÇÒSTĄĘSRŁŹÖ±œÓĐŽłöÂúŚăÌőŒț”ÄÏ߶ÎPQł€¶È”ÄŚîŽóÖ”Łź
ĄŸŽđ°žĄżŁš1Ł©0Ł»![]() ©1Ł»
©1Ł»![]() Ł»
Ł»
Łš2Ł©b”ÄÈĄÖ”·¶Î§ÊÇ©3![]() ĄÜbĄÜ3
ĄÜbĄÜ3![]() Ł»
Ł»
Łš3Ł©Ï߶ÎPQł€¶È”ÄŚîŽóÖ”ÎȘ1+2+1=4Łź
ĄŸœâÎöĄż
ÊÔÌâ·ÖÎöŁșŁš1Ł©žùŸĘ”ă”ÄŚű±êșÍжšÒćœâŽđŒŽżÉŁ»
Łš2Ł©žùŸĘÖ±Ïßy=x+b”ÄÌ۔㣏œáșÏSM=2ŁŹžùŸĘ”ÈŃüÖ±œÇÈęœÇĐΔÄĐÔÖÊœâŽđŁ»
Łš3Ł©žùŸĘTÔÚĄŃOÄÚŁŹÈ·¶šST”Ä·¶Î§ŁŹžùŸĘžűłö”ÄÌőŒțĄąœáșÏÍŒĐÎÇółöÂúŚăÌőŒț”ÄÏ߶ÎPQł€¶È”ÄŚîŽóÖ”Łź
ÊÔÌâœâÎöŁșŁš1Ł©Ąß”ăBŁš1ŁŹ0Ł©ŁŹĄàSB=0ŁŹĄßCŁš1ŁŹ1Ł©ŁŹĄàSC=![]() ©1ŁŹĄßDŁš0ŁŹ
©1ŁŹĄßDŁš0ŁŹ![]() Ł©ŁŹĄàSD=
Ł©ŁŹĄàSD=![]() ŁŹčÊŽđ°žÎȘŁș0Ł»
ŁŹčÊŽđ°žÎȘŁș0Ł»![]() ©1Ł»
©1Ł»![]() ,Ł»
,Ł»
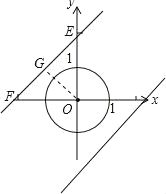
Łš2Ł©ÉèÖ±Ïßy=x+bÓë·Ö±đÓëxÖ᥹yÖ᜻ÓÚFĄąEŁŹŚśOGĄÍEFÓÚGŁŹ
ĄßĄÏFEO=45ĄăŁŹĄàOG=GEŁŹ”±OG=3ʱŁŹGE=3ŁŹ
ÓÉčŽčɶšÀí”ĂŁŹOE=3![]() ŁŹŽËʱֱÏߔĜâÎöÊœÎȘŁșy=x+3
ŁŹŽËʱֱÏߔĜâÎöÊœÎȘŁșy=x+3![]() ŁŹ
ŁŹ
ĄàÖ±Ïßy=x+bÉÏŽæÔÚ”ăMŁŹÊč”ĂSM=2ŁŹb”ÄÈĄÖ”·¶Î§ÊÇ©3![]() ĄÜbĄÜ3
ĄÜbĄÜ3![]() Ł»
Ł»
Łš3Ł©ĄßTÔÚĄŃOÄÚŁŹĄàSTĄÜ1ŁŹĄßSTĄĘSRŁŹĄàSRĄÜ1ŁŹ
ĄàÏ߶ÎPQł€¶È”ÄŚîŽóÖ”ÎȘ1+2+1=4Łź


 șŁ”í»ÆžÔĂûÊŠ”ŒșœÏ”ÁĐŽđ°ž
șŁ”í»ÆžÔĂûÊŠ”ŒșœÏ”ÁĐŽđ°ž ÆŐÍšžßÖĐÍŹČœÁ·Ï°ČáÏ”ÁĐŽđ°ž
ÆŐÍšžßÖĐÍŹČœÁ·Ï°ČáÏ”ÁĐŽđ°ž ÓĆÒíĐĄ°ïÊÖÍŹČœżÚËăÏ”ÁĐŽđ°ž
ÓĆÒíĐĄ°ïÊÖÍŹČœżÚËăÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘaĄąbĄącÎȘĄśABC”ÄÈę±ßŁŹÇÒÂúŚăa2c2©b2c2Łœa4©b4ŁŹÔòĄśABCÊÇŁšĄĄĄĄŁ©
A.Ö±œÇÈęœÇĐÎB.”ÈŃüÈęœÇĐÎ
C.”ÈŃüÈęœÇĐλòÖ±œÇÈęœÇĐÎD.”ÈŃüÖ±œÇÈęœÇĐÎ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚÈçÍŒËùÊŸ”ÄŐę·œĐÎÍűžńÖĐŁŹĂżžöĐĄŐę·œĐΔı߳€ÎȘ1ŁŹžń”ăÈęœÇĐÎŁš¶„”ăÊÇÍűžńÏߔĜ»”ă”ÄÈęœÇĐÎŁ©ABC”Ķ„”ăAŁŹC”ÄŚű±ê·Ö±đÎȘAŁš-4ŁŹ5Ł©ŁŹCŁš-1ŁŹ3Ł©Łź
Łš1Ł©ÇëÔÚÈçÍŒËùÊŸ”ÄÍűžńÄÚŚśłöxÖ᥹yÖ᣻
Łš2Ł©Ç댜łöĄśABCčŰÓÚyÖá¶ÔłÆ”ÄĄśA1B1C1Ł»
Łš3Ł©ĐŽłö”ăB1”ÄŚű±êČąÇółöĄśA1B1C1”ÄĂæ»ęŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
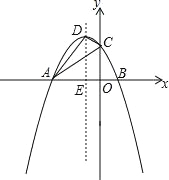
ĄŸÌâÄżĄżÈçÍŒŁŹĆŚÎïÏßy=©x2+bx+cÓëxÖá·Ö±đœ»ÓÚ”ăAŁš©3ŁŹ0Ł©șÍ”ăBŁŹÓëyÖ᜻ÓÚ”ăCŁš0ŁŹ3Ł©ŁŹ¶„”ăÎȘ”ăDŁŹ¶ÔłÆÖáDEœ»xÖáÓÚ”ăEŁŹÁŹœÓADŁŹACŁŹDCŁź
Łš1Ł©ÇóĆŚÎïÏß”ÄșŻÊę±íŽïÊœŁź
Łš2Ł©ĆĐ¶ÏĄśADC”ÄĐÎŚŽŁŹČąË”ĂśÀíÓÉŁź
Łš3Ł©¶ÔłÆÖáDEÉÏÊÇ·ńŽæÔÚ”ăPŁŹÊč”ăP”œÖ±ÏßAD”ÄŸàÀëÓ딜xÖá”ÄŸàÀëÏà”ÈŁżÈôŽæÔÚŁŹÇółö”ăP”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŁșĆŚÎïÏßy=x2+Łš2m©1Ł©x+m2©1ŸčęŚű±êԔ㣏ÇÒ”±xŁŒ0ʱŁŹyËæx”ÄÔöŽó¶űŒőĐĄŁź
Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš2Ł©œáșÏÍŒÏóĐŽłöŁŹ0ŁŒxŁŒ4ʱŁŹÖ±œÓĐŽłöy”ÄÈĄÖ”·¶Î§ Ł»
Łš3Ł©Éè”ăAÊÇžĂĆŚÎïÏßÉÏλÓÚxÖáÏ·œ”ÄÒ»žö¶Ż”㣏čę”ăAŚśxÖá”ÄÆœĐĐÏßœ»ĆŚÎïÏßÓÚÁíÒ»”ăDŁŹÔÙŚśABĄÍxÖáÓÚ”ăBŁŹDCĄÍxÖáÓÚ”ăCŁź”±BC=1ʱŁŹÇółöŸŰĐÎABCD”ÄÖÜł€Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒ»ŚéÊęŸĘ2ŁŹ©4ŁŹxŁŹ6ŁŹ©8”ÄÖÚÊęÎȘ6ŁŹÔòŐâŚéÊęŸĘ”ÄÖĐλÊęÎȘ______Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżœ«¶àÏîÊœx3-5xy2-7y3+8x2y°ŽÄłÒ»žöŚÖÄž”ÄÉęĂĘĆĆÁĐŁŹŐęÈ·”ÄÊÇŁšŁ©
A. x3-7y3-5xy2+8x2y B. -7y3-5xy2+8x2y+x3 C. 7y3-5xy2+8x2y+x3 D. x3-5xy2+8x2y-7y3
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
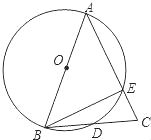
ĄŸÌâÄżĄżÒŃÖȘŁșÈçÍŒŁŹABÎȘĄŃO”ÄÖ±Ÿ¶ŁŹAB=ACŁŹBCœ»ĄŃOÓÚ”ăDŁŹACœ»ĄŃOÓÚ”ăEŁŹĄÏBAC=45ĄăŁź
Łš1Ł©ÇóĄÏEBC”ĶÈÊꣻ
Łš2Ł©ÇóÖ€ŁșBD=CDŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
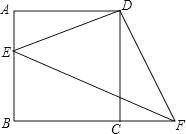
ĄŸÌâÄżĄżÈçÍŒŁŹËıßĐÎABCDÊÇŐę·œĐÎŁŹE”ăÔÚABÉÏŁŹF”ăÔÚBC”ÄŃÓł€ÏßÉÏŁŹÇÒCF=AEŁŹÁŹœÓDEĄąDFĄąEFŁź
ąÙÇóÖ€ŁșĄśADEĄŐĄśCDFŁ»
ąÚÌîżŐŁșĄśCDFżÉÒÔÓÉĄśADEÈÆĐęŚȘÖĐĐÄ ”㣏°ŽÄæʱŐë·œÏòĐęŚȘ ¶È”Ă”œŁ»
ąÛÈôBC=3ŁŹAE=1ŁŹÇóĄśDEF”ÄĂæ»ęŁź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com