
已知关于的方程 与
与 都有实数根,若这两个方程有且只有一个公共根,且
都有实数根,若这两个方程有且只有一个公共根,且 ,则称它们互为“同根轮换方程”.如
,则称它们互为“同根轮换方程”.如 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.
(1)若关于 的方程
的方程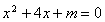 与
与 互为“同根轮换方程”,求
互为“同根轮换方程”,求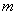 的值;
的值;
(2)若 是关于
是关于 的方程
的方程 的实数根,
的实数根, 是关于
是关于 的方程
的方程 的实数根,当
的实数根,当 .
. 分别取何值时,方程
分别取何值时,方程 与
与 互为“同根轮换方程”,请说明理由.
互为“同根轮换方程”,请说明理由.
(1)m=-12;(2)当p=q=-3a时,方程 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.
【解析】
试题分析:(1)根据同根方程条件:两个方程有且只有一个公共根,且 ,先求出公共根,进而求出
,先求出公共根,进而求出 的值;
的值;
(2)仿照(1)的过程求出 .
. 的取值,只要得到p=q,2a×
的取值,只要得到p=q,2a× b=ab,即可判断方程
b=ab,即可判断方程 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.
试题解析:(1)∵方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,
∴ 4m=-6n.
设t是公共根,则有t2+4t+m=0,t2-6t+n=0.
解得,t= .
.
∵4m=-6n.
∴t= .
.
∴( )2+4(
)2+4( )+m=0.
)+m=0.
∴m=-12.
(2)若方程x2+ax+b=0(b≠0)与 有公共根.
有公共根.
则由x2+ax+b=0, 解得x=
解得x= .
.
∴ .
.
∴b=-6a2.
当b=-6a2时,有x2+ax-6a2=0,x2+2ax-3a2=0.
解得,x1=-3a,x2=2a;x3=-3a,x4=a.
若p=q=-3a,
∵b≠0,∴-6a2≠0,∴a≠0.
∴2a≠a.即x2≠x4.
∵2a× b=ab,
b=ab,
∴方程x2+ax+b=0(b≠0)与 =0互为“同根轮换方程” .
=0互为“同根轮换方程” .
考点:一元二次方程的应用.1061442


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| a |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2k+1 |
| 2k+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com